Aufgabe:
Der Sommer 2019 brachte in Deutschland neue Hitzerekorde. Insbesondere im Juli stieg die Temperatur an vielen Orten auf über \( 40^{\circ} \mathrm{C} \) an. Zur Modellierung der Lufttemperatur (kurz: Temperatur) in Köln am 25.Juli 2019 zwischen 6:00 Uhr und 21:00 Uhr wird für \( 6 \leq t \leq 21 \) die Funktion \( f \) mit
\( f(t)=0,00265 \cdot t^{4}-0,1428 \cdot t^{3}+2,5116 \cdot t^{2}-15,44 \cdot t+54,73,\quad t \in \mathbb{R} \)
verwendet. Dabei gibt \( t \) die Uhrzeit an ( \( t=6 \) entspricht 6:00 Uhr, \( t=7 \) entspricht 7:00 Uhr usw.). \( f(t) \) ist die Temperatur in Köln in \( { }^{\circ} \mathrm{C} \) zu der durch \( t \) gegebenen Uhrzeit. Der Graph on \( f \) ist für \( 6 \leq t \leq 21 \) in der Abbildung dargestellt.
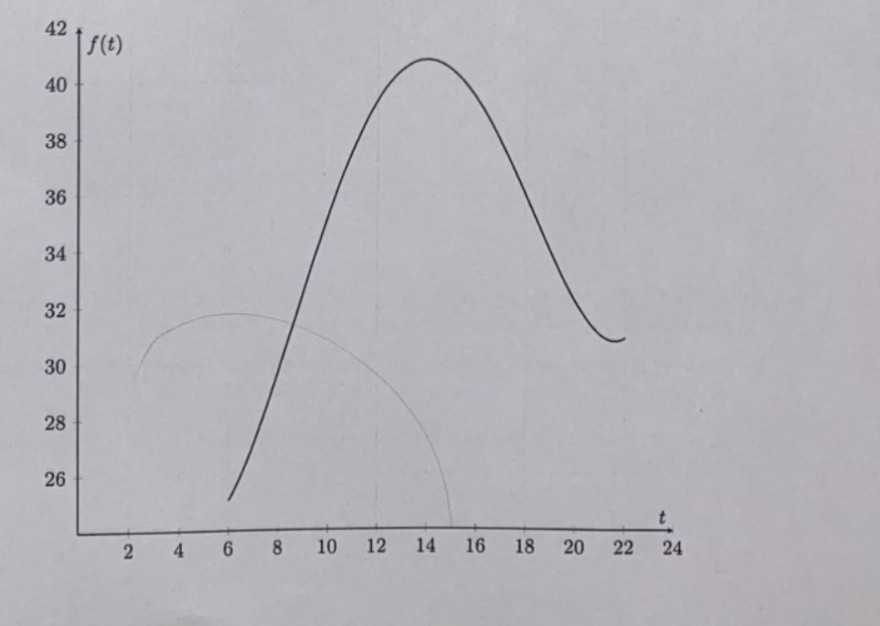
d) Ermitteln Sie rechnerisch die niedrigste und die höchste Temperatur im betrachteten Zeitraum von 6:00 Uhr bis 21:00 Uhr.
In der folgenden Aufgabe e) wird nun der Temperaturverlauf am 25.Juli 2019 in Köln für die Zeiträume vor 6:00 Uhr und nach 21:00 Uhr betrachtet.
e)
(i) Begründen Sie, dass die Funktion \( f \) nicht zur Modellierung des Temperaturverlaufs für den gesamten Zeitraum von 0:00 Uhr bis 6:00 Uhr geeignet ist.
(ii) Für den Zeitraum von 21:00 Uhr bis 24:00 Uhr geht man davon aus, dass die Temperatur gleichmäßig mit der monıentanen Änderungsrate abnimmt, die um 21:00 Uhr vorliegt. Ermitteln Sie unter dieser Annahme die Temperatur in Köln um 24:00 Uhr.
Problem/Ansatz:
Wie kann ich rechnerisch die niedrigste und die höchste Temperatur im angegebenen Zeitraum berechnen? Aufgabe 4 d.
Wie rechne ich Aufgabe E (1 und 2)