Soll damit vielleicht gemeint sein, dass das arithmetische Mittel der Schnittpunkte den x-Wert ergibt?
Das ist bei der Aufgabe zufällig so. Siehe auch die weiteren Ausführungen.
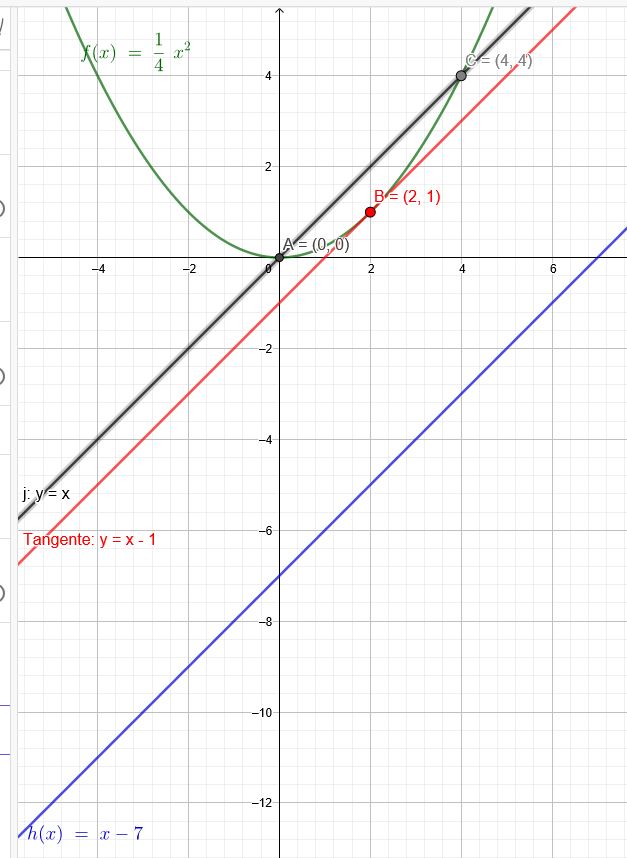
Mit deiner mir seltsam erscheinenden Rechnung bestimmst du die Schnittstellen beider Funktionsgraphen, nämlich x=0 und x=4.
Ich beginne mit dem Verfahren zur Schnittpunktebestimmung. Breche dieses aber nach der Aufstellung der Klammer \((x-a)^2\) ab. \(a\) ist nun die Berührstelle der gesuchten Tangente. Schneidet eine Gerade nirgends die Parabel gilt auch das bei \((x-a)^2\) Gesagte.
Es sei nun \(f(x)= \frac{1}{4}x^2 \) und \(g(x)=x-7\)
\( \frac{1}{4}*x^2=x-7\)
\( x^2-4x=-28\)
\( (x-2)^2=-28+4=-24=24i^2 |\sqrt{~~}\)
1.)
\( x-2=2i\sqrt{6} \)
\( x_1=2+2i\sqrt{6} \)
2.)
\( x-2=-2i\sqrt{6} \)
\( x_2=2-2i\sqrt{6} \)
Die Schnittpunkte der Geraden liegen hier ∈ ℂ.
Der Berührpunkt der parallelen Tangente ist \(B(2|1)\)