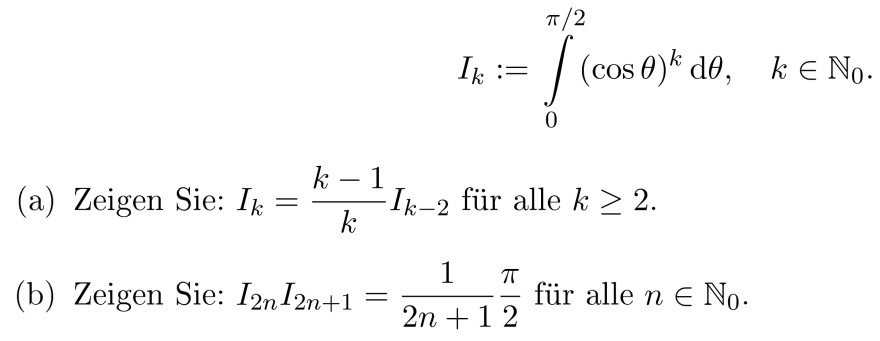
Text erkannt:
\( I_{k}:=\int \limits_{0}^{\pi / 2}(\cos \theta)^{k} \mathrm{~d} \theta, \quad k \in \mathbb{N}_{0} \)
(a) Zeigen Sie: \( I_{k}=\frac{k-1}{k} I_{k-2} \) für alle \( k \geq 2 \).
(b) Zeigen Sie: \( I_{2 n} I_{2 n+1}=\frac{1}{2 n+1} \frac{\pi}{2} \) für alle \( n \in \mathbb{N}_{0} \).
Aufgabe:
Problem/Ansatz:
Ich habe leider keine Idee. Wäre lieb wenn jemand helfen könnte.