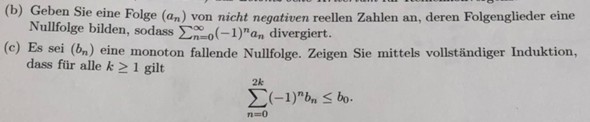
Text erkannt:
(b) Geben Sie eine Folge \( \left(a_{n}\right) \) von nicht negativen reellen Zahlen an, deren Folgenglieder eine Nullfolge bilden, sodass \( \sum \limits_{n=0}^{\infty}(-1)^{n} a_{n} \) divergiert.
(c) Es sei \( \left(b_{n}\right) \) eine monoton fallende Nullfolge. Zeigen Sie mittels vollständiger Induktion, dass für alle \( k \geq 1 \) gilt
\( \sum \limits_{n=0}^{2 k}(-1)^{n} b_{n} \leq b_{0} \)
Kann mir jemand bei dieser Aufgabe helfen? Komme nicht weiter!