Lösen von Gleichungssystemen

Question

Aufgabe:

"Gib an wie viele Lösungen die folgenden Gleichungssysteme jeweils haben. Begründe deine Antwort und gib ggf. eine Lösung an."

a)

I) \( 2 x-y+4 z=5 \)
II) \( 5 x+2 y-10 z=7 \)
III) \( 12 x-9 y-8 z=11 \)

b)

I) \( 4 x+7 y-3 z=6 \)
II) \( -3 x-5 y+z=7 \)
II) \( -8 x-14 y+6 z=-12 \)

c)

I) \( -2 x+4 y+10 z=12 \)
II) \( 6 x+3 y-7 z=4 \)
III) \( x-2 y-5 z=-7 \)

Problem/Ansatz:

Ich weiß nicht so ganz woher man auf den ersten Blick sehen kan, wie viele Lösungen es hat ohne zu rechnen... Und beim zweiten sieht man dass sich die Vorfaktoren verdoppeln und beim letzten halbieren. Aber beim ersten seh ich da nicht so richtig den Zusammenhang. Kann mir da jemand bitte helfen?

Comments

Sollst du denn auf den 1. Blick die Anzahl der Lösungen nennen?

---

Also auf den 'ersten Blick' ist es bei a) genau eine Lösung, bei b) unendlich viele und bei c) gar keine.

Wenn ich mich nicht 'verblickt' habe ;-)

---

Und wie hast du das entschlumpft?

---

Ah, danke! Also ich hab jetzt das zweite und letzte verstanden. Auf das erste komme ich nur, wenn ich rechne. Wie hast du es geschafft, so schnell herauszubekommen, dass das Gleichungssystem genau eine Lösung hat?

---

"Gib an wie viele Lösungen die folgenden Gleichungssysteme jeweils haben. Begründe deine Antwort und gib ggf. eine Lösung an."

Bei 1) sieht man das nicht sofort (vgl. Mathecoach)

Aber wo steht denn in der Aufgabe eigentlich, dass dass man die Lösungsmenge 'auf einen Blick' erkennen soll?

---

Und wie hast du das entschlumpft?

von hinten nach vorn:

zu c) betrachtet man \(-2\cdot \text{III)}\) und vergleicht mit \(\text{I)}\), dann steht dort \(12 = -14\), was nicht sein kann.

zu b) hier ist \(-2\cdot \text{I)} = \text{III)}\). Damit verbleiben zwei Gleichungen (die sich nicht "widersprechen") mit drei Unbekannten.

zu a) zugegeben: auf den ersten Blick habe ich mutig geraten. Auf den zweiten Blick kann man es aber "sehen": Dass die drei Gleichungen paarweise unabhängig sind, kann man ohne weiteres sehen.

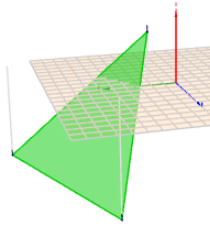
Weiter stelle mir jede Zeile(!) als Punkt im Raum vor. Die drei X-Koordinaten sind alle positiv, liegen also auf einer Seite der YZ-Ebene. Und die Y- und Z-Koordinaten sind über drei Quadranten verteilt. Damit bilden sie ein Dreibein, was eine Ebene aufspannt, die nicht durch den Ursprung verläuft. Die Gerade, die durch \(\text{I)}\) und \(\text{II)}\) knapp über ('über' in X-Richtung) dem Ursprung verläuft ist noch 'hoch' genug (bei \(2x\) und \(5x\)), so dass der Ursprung sicher 'draußen' ist.

Daraus folgt, dass es genau eine Lösung gibt.

Und das stelle ich mir dabei (im Kopf!) vor:

---

zur Kontrolle:

https://www.arndt-bruenner.de/mathe/scripts/gleichungssysteme.htm

---

Silvia hat "entschlumpft" gesagt <3

Answer 1

woher man auf den ersten Blick sehen kan, wie viele Lösungen es hat ohne zu rechnen

Auf den ersten Blick landen die Informationen im sensorischen Gedächtnis. Im sensorischen Gedächtnis wird den Objekten keine Bedeutung zugemessen. Ich halte es für ausgeschlossen, die Anzahl der Lösungen eines LGS zu erkennen, ohne den Objekten eine Bedeutung zuzumessen.

Answer 2

Bei b) sieht man recht deutlich, dass die 3. Zeile ein Vielfaches der ersten Zeile ist. Damit kann man die 3. Zeile streichen und es gibt unendlich viele Lösungen.

Bei c) sieht man, dass die 3. Zeile der Koeffizienten ein Vielfaches der ersten Zeile ist, die Konstante aber ein nicht dieses Vielfache ist. Damit gibt es dort keine Lösung.

Bei a) kann man das meiner Meinung nach nicht direkt sehen. Hier könnte ja die 3 Zeile auch eine Linearkombination der ersten beiden Zeilen sein. Daher könnte man die Determinante der Koeffizientenmatrix bilden. Dann sieht man, dass diese nicht Null ist und es genau eine Lösung geben muss. Natürlich könnte man die Determinante überschlagen, aber ohne wirklich zu rechnen, wüsste ich da keinen Weg.

Da du aber ohnehin eine Lösung angeben sollst, kommst du vermutlich eh nicht ohne eine Rechnung aus.

Comments

Wie bildet man die Determiante der Koeffizientenmatrix?