Aufgabe:
Allgemeine Frage zum Lösen von Linearen Gleichungssystemen mit 3 Unbekannten
Problem/Ansatz:
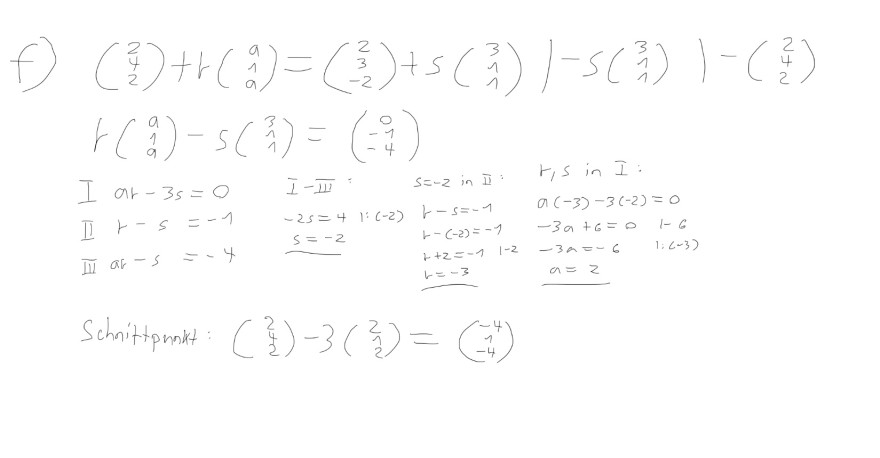
Im Zuge einer Schulaufgabe habe ich folgendes LGS gelöst (2 Geradengleichungen in Vektorform gleichgesetzt). Mir kam nun aber trotz keinerlei Lösungs-Schwierigkeiten folgende Frage auf:
Ich habe im ersten Schritt die erste Gleichung mit der dritten Gleichung subtrahiert (Gauß-Algorithmus), dann das erhaltene s in die zweite Gleichung eingesetzt, um r zu erhalten und die dadurch bekannten Werte r und s schließlich in die erste Gleichung eingesetzt.
Nun meine ich mich zu erinnern, dass es Gleichungssysteme gibt, bei der man die Richtigkeit der erhaltenen Parameter überprüft, indem man diese in eine unbenutzte Gleichung einsetzt. In meinem Beispiel gibt es ja aber eigentlich keine unbenutzte Gleichung, alleine schon weil ich Gleichung 1 und 3 miteinander verrechnet habe und dann in Gleichung 2 eingesetzt habe.
Oder muss ich die beiden Werte eigentlich noch mithilfe von Gleichung 3 überprüfen, da ich hier noch nichts eingesetzt habe (habe ich bereits gemacht, geht auf.)
Würde mich über eine Erklärung dazu freuen, in welchen Fällen eine Überprüfung der erhaltenen Parameter notwendig ist.