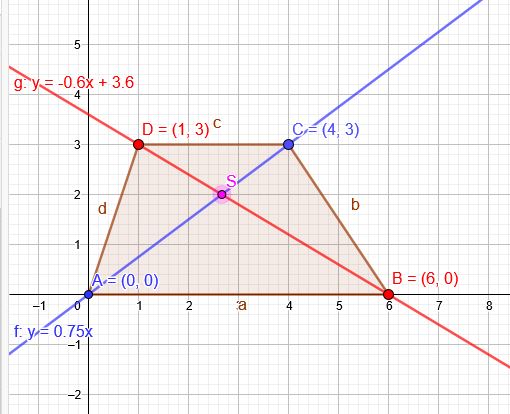
Geradengleichungen mit den Mitteln deiner Wahl.
Koordinaten von S:
\(y= \frac{3}{4}x \) geschnitten mit \(y=- \frac{3}{5}x+\frac{18}{5} \)
\(\frac{3}{4}x=- \frac{3}{5}x+\frac{18}{5} \)
\(\frac{3}{4}x+ \frac{3}{5}x=\frac{18}{5} \)
\(\frac{27}{20}x=\frac{18}{5} |:9 \)
\(\frac{3}{20}x=\frac{2}{5} |\cdot \frac{20}{3} \)
\(x=\frac{2}{5} \cdot \frac{20}{3}=\frac{8}{3} \) \(y=\frac{3}{4} \cdot \frac{8}{3}=2\)
S\((\frac{8}{3}|2)\)
Strecke AS \( \sqrt{(\frac{8}{3})^2+2^2}=\sqrt{\frac{100}{9}}=\frac{10}{3} \)
Strecke SC \( \sqrt{(4-\frac{8}{3})^2+(3-2)^2}=\sqrt{\frac{25}{9}}=\frac{5}{3} \)
\( \frac{ AS}{SC}=\frac{\frac{10}{3} }{\frac{5}{3}}=\frac{2 }{1} \)
Analog \( \frac{ BS}{SD} \) berechnen.