Aufgabe:
Berechne den Median
Problem/Ansatz:
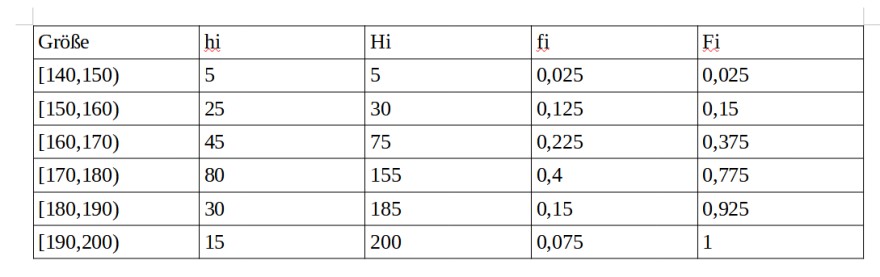
Text erkannt:
\begin{tabular}{|l|l|l|l|l|}
\hline Größe & hi & Hi & fi & Fi \\
\hline\( [140,150) \) & 5 & 5 & 0,025 & 0,025 \\
\hline\( [150,160) \) & 25 & 30 & 0,125 & 0,15 \\
\hline\( [160,170) \) & 45 & 75 & 0,225 & 0,375 \\
\hline\( [170,180) \) & 80 & 155 & 0,4 & 0,775 \\
\hline\( [180,190) \) & 30 & 185 & 0,15 & 0,925 \\
\hline\( [190,200) \) & 15 & 200 & 0,075 & 1 \\
\hline
\end{tabular}
Wenn man sich die Relative Kummulierte Häufigkeit(Fi) ansieht, dann erkennt man, dass die am naheliegendsten Stelle im dritten Intervall bei 0,375 ist. 0,375 sind 37,5%. Der Median liegt bei 50%. Wenn wir uns den vierten Intervall anschauen, dann beginnt dieses bei 37,5% und endet bei 0,775 sprich 77,5%. Das das heißt, im vierten Intervall fehlen 12,5%, damit man den Median erreicht und der Median liegt im vierten Intervall. Eine Weitere Information die mir aufgefallen ist, dass das Intervall 10 cm Breit ist, das heißt von 170-180. Auf diesen 10cm liegen 40% der Werte, wie komme ich auf 40%? Nun das Intervall startet ja bei 170 und 170=37,5% und es endet bei 180 sprich 77,5%. Die Differenz daraus sind 40%.
Wie berechne ich nun den Median mit den ganzen Informationen, die mir aufgefallen sind?
