Orden Sie den Funktionen den Graphen zu

Question

Aufgabe:

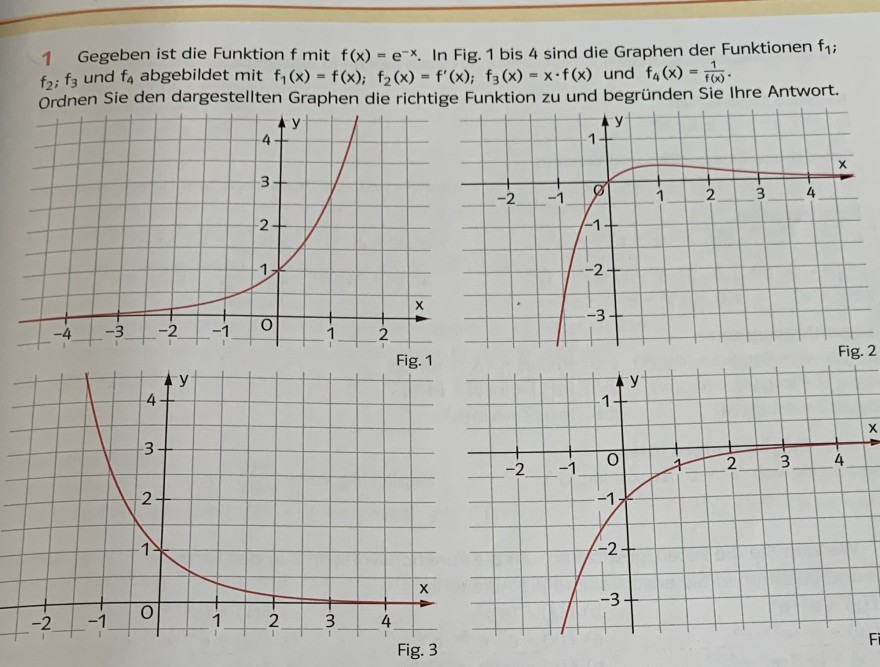
Gegeben ist die Funktion f mit f(x) = e^-x. In Fig. 1 bis 4 sind die Graphen der Funktionen f1;
f2; f3 und f4 abgebildet mit f1(x) = f(x); f2 (x) = f'(x); f3(x) = x * f(x) und f4 (x) = 1/f(x)
Ordnen Sie den dargestellten Graphen die richtige Funktion zu und begründen Sie Ihre Antwort.

Text erkannt:

1 Gegeben ist die Funktion \( f \) mit \( f(x)=e^{-x} \). In Fig. 1 bis 4 sind die Graphen der Funktionen \( f_{1} \); \( f_{2} ; f_{3} \) und \( f_{4} \) abgebildet mit \( f_{1}(x)=f(x) ; f_{2}(x)=f^{\prime}(x) ; f_{3}(x)=x \cdot f(x) \) und \( f_{4}(x)=\frac{1}{f(x)} \).
Ordnen Sie den dargestellten Graphen die richtige Funktion zu und begründen Sie Ihre Antwort.
Fig. 1
Fig. 3

Problem/Ansatz:

Ich weiß bei der Aufgabe leider überhaupt nicht weiter nur habe keine Idee, wie ich da zu einer Lösung kommen könnte. Da ich das für die anstehende Klausur benötige, würde ich mich ganz doll freuen, wenn mir jemand dabei helfen könnte und es mir auch erklären könnte, warum, damit ich es nachvollziehen kann. Das wäre sehr nett über vielleicht fällt es einem ja sehr leicht.

Answer 1

f1: Fig. 3 --> ist die Originalfunktion y = e^{-x}. Die sollte man schon können genau wie y = e^x

f2: Fig. 4 → Gesucht ist der Steigungsgraf von Fig.3. Da der Graph in Fig. 3 für alle x fällt erwarten wir beim Steigungsgrafen nur negative Funktionswerte.

f3: Fig. 2 → Wenn man etwas mit x multipliziert dann bekommt man eine Nullstelle für x = 0 nach dem Satz vom Nullprodukt.

f4: Fig. 1 → Man bildet den Kehrwert der Funktion. Damit kann man auch einfach den Exponenten im Vorzeichen ändern und dann hat man y = e^x die man ebenso kennen sollte.