Vom Duplikat:
Titel: Preisfunktion IN GEOGEBRA erstellen und Steigung im Sachzusammenhang erklären und Regressionskurve bestimmen
Stichworte: geogebra,preisabsatzfunktion,kubisch,quadratische,regression
Aufgabe: 
Preisfunktion p(x) = 216 - 0,48x
Wenn 100 Personen bereit wären, für das Produkt 200 € zu zahlen und man den Preis um 40 € senkt, so erhöht sich der Umsatz auf das 8 fache. a. Erstellen Sie die dazugehörige Preisfunktion
Problem/Ansatz: Hier stehe ich leider total an, vorallem weil ich es in GEOGEBRA MACHEN MUSS.
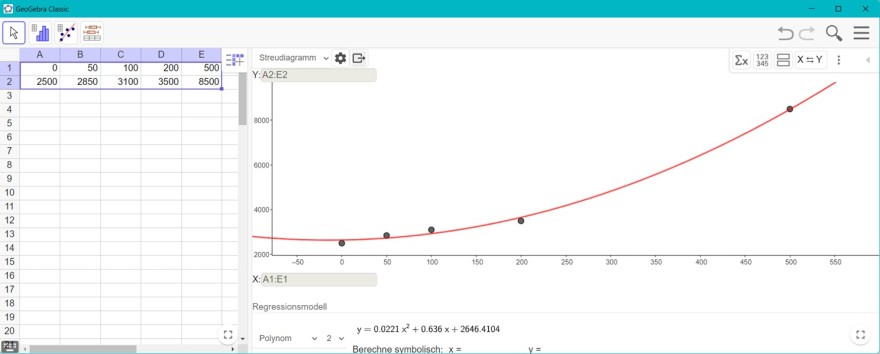
An folgender Tabelle kann man den Zusammenhang zwischen Produktionsmenge und Gesamtkosten erkenne:
Produktionsmenge 0 50 100 200 500
2500 2850 3100 3500 8500
b. Bestimmen Sie zu diesen Daten die quadratische und kubische Regressionsfunktionskurve.
mein Versuch, weiß nicht ob stimmt