Aufgabe: Stetigkeit von Funktionen. Es gelte die Funktion (siehe Foto). Zu zeigen ist, dass die Funktion in jedem
x ∈ [0, 1] \ {0} unstetig ist mit der Definition von Stetigkeit
Problem/Ansatz: Ich komme da irgendwie mit den Bedingungen nicht klar, ob x aus IR ist bzw. IR \ Q. Kann mir da jemand helfen?
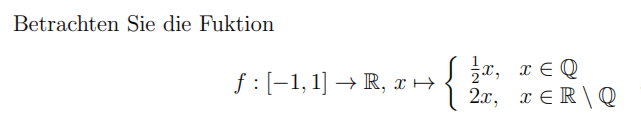
Text erkannt:
Betrachten Sie die Fuktion
\( f:[-1,1] \rightarrow \mathbb{R}, x \mapsto\left\{\begin{array}{ll} \frac{1}{2} x, & x \in \mathbb{Q} \\ 2 x, & x \in \mathbb{R} \backslash \mathbb{Q} \end{array}\right. \)
