Geben Sie mit Vektoren Wege an

Question

Aufgabe:

Eine Spinne auf der Jagd
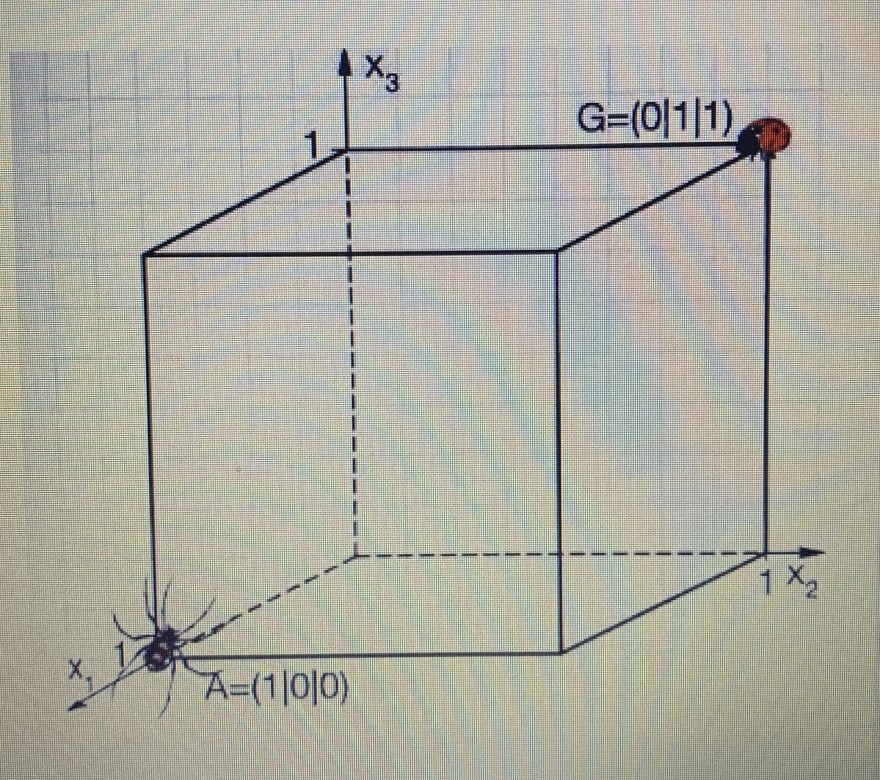
Eine Spinne läuft auf einem Würfel von A zum Käfer am gegenüberliegenden Punkt G (Abb. 1).
Geben Sie mit Hilfe von Vektoren drei möglichst kurze Wege von A nach G an.

Problem/Ansatz:

Mein Ansatz wäre es, die Aufgabe mit dem Ortsvekort AG zu lösen. Allerdings weiß ich nicht genau, wie ich die x1,2,3-Koordinate da ablesen kann und würde mich daher über ein Beispiel freuen, damit ich weiß, wie ich die anderen 2 kurzen Wege angeben kann.

Comments

läuft auf einem Würfel

Also nicht diagonal durch den Würfel und auch nicht zwingend den Würfelkanten entlang.

Answer 1

\(\vec{AG} = \begin{pmatrix}0\\0\\1\end{pmatrix} + \begin{pmatrix}0\\1\\0\end{pmatrix} + \begin{pmatrix}-1\\0\\0\end{pmatrix}\)

Die anderen zwei Wege bekommst du über das Kommutativgesetz.

Comments

Geben Sie mit Hilfe von Vektoren drei möglichst kurze Wege von A nach G an.

$$AG = G-A = \begin{pmatrix} 0\\ 1\\ 1\end{pmatrix} - \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} = \begin{pmatrix} -1\\ 1\\ 1\end{pmatrix}$$und ein kurzer Weg (auf dem Würfel) von \(A\) nach \(G\) wäre:$$\begin{pmatrix} 0\\ 1\\ 0,5\end{pmatrix} + \begin{pmatrix} -1\\ 0\\ 0,5 \end{pmatrix}= \begin{pmatrix} -1\\ 1\\ 1\end{pmatrix}$$

---

Ich glaube nicht, dass die Spinne es sich zutraut, quer durch eine Seitenfläche zu laufen. Das ist viel zu gefährlich.

Answer 2

drei möglichst kurze Wege: grün, rot und blau

Comments

Vielen Dank für die Hilfe. Ich verstehe nur nicht so ganz, wie ich da jetzt als Vektor schreiben kann, weil ich da nur jeweils 2 Koordinaten pro Weg ablesen kann. Könnten Sie mir das vielleicht kurz erklären?

---

Ich verstehe nur nicht so ganz, wie ich da jetzt als Vektor schreiben kann, weil ich da nur jeweils 2 Koordinaten pro Weg ablesen kann

so wie es schon in meinem Kommentar unter der Antwort von oswald steht (siehe dort). Genauso verläuft hier z.B. der grüne Weg:$$\begin{pmatrix} 0\\ 0,5\\ 1\end{pmatrix} + \begin{pmatrix} -1\\ 0,5\\ 0 \end{pmatrix}= \begin{pmatrix} -1\\ 1\\ 1\end{pmatrix}$$(klick hier)

Die dritte Koordinate, die senkrecht auf der jeweiligen Fläche steht, ist dann 0.

---

Da sind mir zwei Kollegen, Werner-Salomon und Der_Mathecoach (in chronologischer Reihenfolge), mit einer Antwort zuvorgekommen.

Du kannst Dir anschaulich vorstellen, dass es die kürzesten Wege sind, wenn Du die beiden Würfelseiten über die sie führen aufklappst, in eine Ebene. Die kürzeste Verbindung zwischen zwei Punkten ist eine Gerade. Meine drei farbigen Linien sind nach dem Aufklappen jeweils auf einer Geraden.

---

Vielen Dank für die ganzen Erklärungen! Jetzt habe ich es verstanden. Ich musste nur erstmal wieder ins Thema reinkommen, weil wir es zuletzt vor über einem Jahr behandelt haben.

Answer 3

Vielen Dank für die Hilfe. Ich verstehe nur nicht so ganz, wie ich da jetzt als Vektor schreiben kann, weil ich da nur jeweils 2 Koordinaten pro Weg ablesen kann. Könnten Sie mir das vielleicht kurz erklären?

Die drei Wege die döschwo auf dem Würfel skizziert hat sind

$$\overrightarrow v_{rot} = \begin{pmatrix} -0.5\\0\\1 \end{pmatrix} + \begin{pmatrix} -0.5\\1\\0 \end{pmatrix} \newline \overrightarrow v_{grün} = \begin{pmatrix} 0\\0.5\\1 \end{pmatrix} + \begin{pmatrix} -1\\0.5\\0 \end{pmatrix} \newline \overrightarrow v_{blau} = \begin{pmatrix} -0.5\\1\\0 \end{pmatrix} + \begin{pmatrix} -0.5\\0\\1 \end{pmatrix}$$

Dieses sind auch 3 der 6 kürzesten Wege auf dem Würfel.