Finden Sie alle reellen Lösungen des Differentialgleichungssystems

Question

Aufgabe:

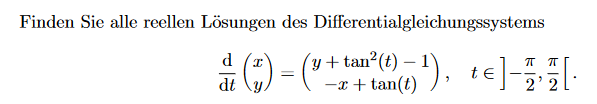
Text erkannt:

Finden Sie alle reellen Lösungen des Differentialgleichungssystems
\( \left.\frac{\mathrm{d}}{\mathrm{d} t}\left(\begin{array}{l} x \\ y \end{array}\right)=\left(\begin{array}{c} y+\tan ^{2}(t)-1 \\ -x+\tan (t) \end{array}\right), \quad t \in\right]-\frac{\pi}{2}, \frac{\pi}{2}[ \)

Problem/Ansatz:

also meines wissens nach sind die Schritte:

1) Das charakteristische Polynom finden

2) Die Eigenwerte zu erhalten

3) Eigenvektoren

4) Fundamentalsystem Lösen

5) AWP lösen

ich habe für 1) lamda^2 +1 = 0

das problem ist nur das ich mit dem Ergebnis nicht weiterkomme. Ich vermute ich habe ein Fehler. Ich hoffe jemand kann mir dabei Helfen diese Lösung rauszubekommen gegebenenfalls mit rechenschritten damit ich es nachvollziehen kann

Comments

Du hast kein Problem. Die Eigenwerte sind i und -i (komplex). Dazu musst Du die Eigenvektoren bestimmen. Dann muss Du in Deinem Skript nachlesen, wie man daraus die reellen Lösungen erhält (bzw. ob Ihr erstmal mit den komplexen Lösungen weiterrechnen sollt)....

Answer 1

Hallo,

λ^2 +1 = 0 stimmt

habe es über einen anderen Weg berechnet.

Ansatz part. Lösung via Variation der Konstanten.