Die Normale schließt ein Dreieck ein

Question

Aufgabe:

Gegeben ist die Funktion f(x)=ln(2x-5)

Die Normale h an den Graphen der Funktion im Punkt S(3|0) schließt mit den beiden Koordinatenachsen ein Dreieck ein.

Berechnen Sie den Flächeninhalt dieses Dreiecks

Problem/Ansatz:

Das muss ich doch zuerst die Normal berechnen oder? Wie mache ich das?

Answer 1

Normalemgleichung:

n(x) = (x-3)*f '(3) + 0

f '(x) = 2/(2x-5)

Berechne: n(0) = ---

A= 3*n(0)/2

Answer 2

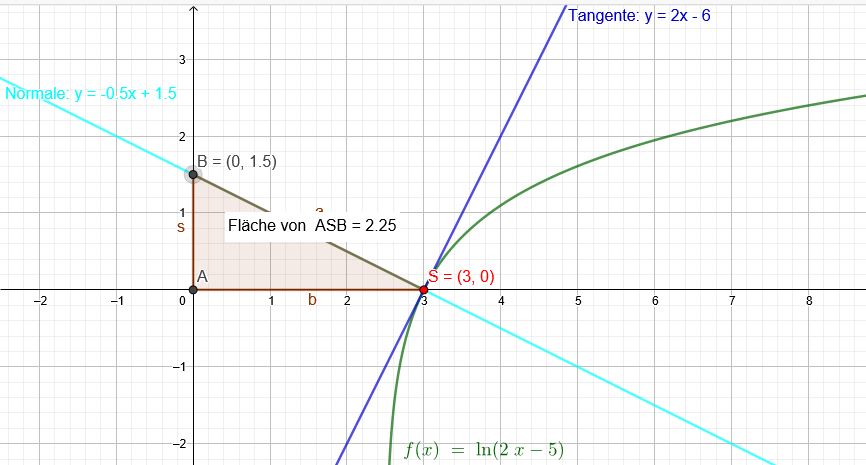
Steigung der Tangente an \(f(x)=ln(2x-5)\)

\(f´(x)=\frac{2}{2x-5}\)

\(S(3|0)\)

\(f´(3)=\frac{2}{2*3-5}=2\)

Steigung der Normalen ist \(m=- \frac{1}{2} \)

Gleichung der Normalen in \(S(3|0)\)

\( \frac{y-0}{x-3}=- \frac{1}{2} \)

Diese Normale schneidet die y-Achse in

\( \frac{y}{0-3}=- \frac{1}{2} \)

\( y= \frac{1}{2}*3=1,5 \)

\(A=\frac{1}{2}*3*1,5=2,25FE\)