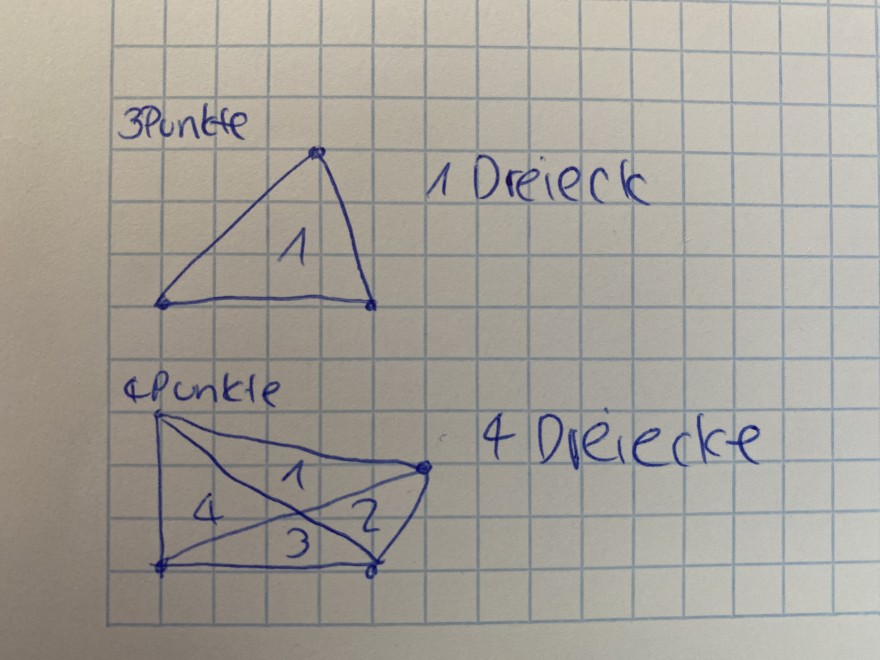
Wenn man 3 Punkte durch Strecken verbindet, erhält man ein Dreieck. Mit 4 Punkten kann man bereits 4 Dreiecke erhalten.
Meine Frage ist wie viele Dreiecke oder auch andere Vielecke erhält man höchstens wenn man 5, 6 und 7 Punkte miteinander verbindet?
Problem/Ansatz:
Wie finde ich das heraus und was sind die Lösungen?