Sind die Zahlen z_{1}=0 und z_{2}=1-{i} in M enthalten?

Question

Aufgabe:

Skizzieren Sie die Menge $$ M=\left\{z \in \mathbb{C}:\: \left|z+\mathrm{i}\right| \leq 1 \:\land\: \operatorname{Im} z+1>0\right\} $$ in der Gaußschen Zahlenebene. Sind die Zahlen \( z_{1}=0 \) und \( z_{2}=1-\mathrm{i} \) in \( M \) enthalten?

Wie würde man das zeichnen?

Answer 1

\(|z-z_0|\) ist der Abstand von \(z\) zu \(z_0\).

\(|z+i|\leq 1\) beschreibt also die Menge aller \(z\),

deren Abstand zu \(-i\) höchstens 1 ist. Diese Menge ist

der Vollkreis mit Radius \(1\) und Mittelpunkt \(-i\).

Die zweite Bedingung dürfte kein Problem sein.

Answer 2

Aloha :)

Schreibe \((z=x+iy)\) mit Realteil \(x\) und Imaginärteil \(y\):

$$|z+i|\le1\implies|x+iy+i|\le1\implies|x+i(y+1)|\le1\implies$$$$\sqrt{x^2+(y+1)^2}\le1\implies x^2+(y+1)^2\le1$$

Das ist die Fläche eines Kreises mit Mittelpunkt \((0|-1)\) und Radius \(1\).

$$\operatorname{Im}(z)+1>0\implies y+1>0\implies y>-1$$Das ist die Halbebene oberhalb der Geraden \(y=-1\) ohne Rand, das heißt \((y=-1)\) selbst gehört nicht dazu. Das heißt, wir haben nur die obere Hälfte des Halbkreises zu berücksichtigen.

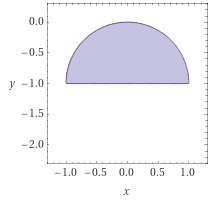
Die Zahl \(z_1=0\), also der Punkt \((0|0)\), ist in \(M\) enthalten.

Die Zahl \((z_2=1-i)\), also der Punkt \((1|-1)\), ist nicht in \(M\) enthalten, da der "Rand" \((y=-1)\) ja nicht zu \(M\) gehört.