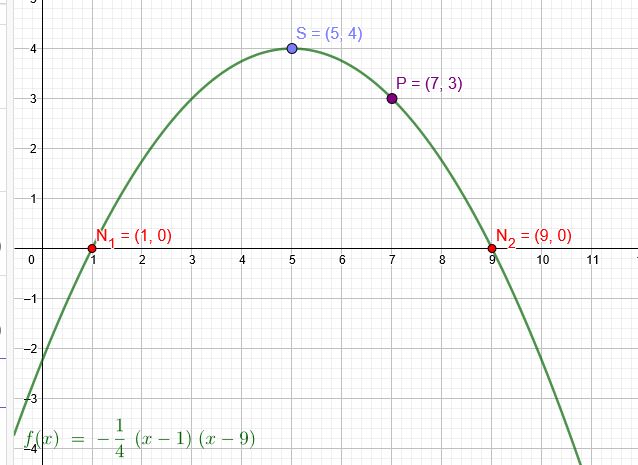
"Wie lautet die Gleichung der Torbogenparabel?"
Lösung mittels Nullstellenform der Parabel, wenn keine Vorgaben zu beachten sind:
\(N_1(1|0)\) \(N_2(9|0)\) \(S(5|4)\) \(P(7|3)\)
\(f(x)=a*(x-1)*(x-9)\)
\(f(5)=a*(5-1)*(5-9)=4\) \(4a*(-4)=4\) \(a=-\frac{1}{4}\)
\(f(x)=-\frac{1}{4}*(x-1)*(x-9)\)