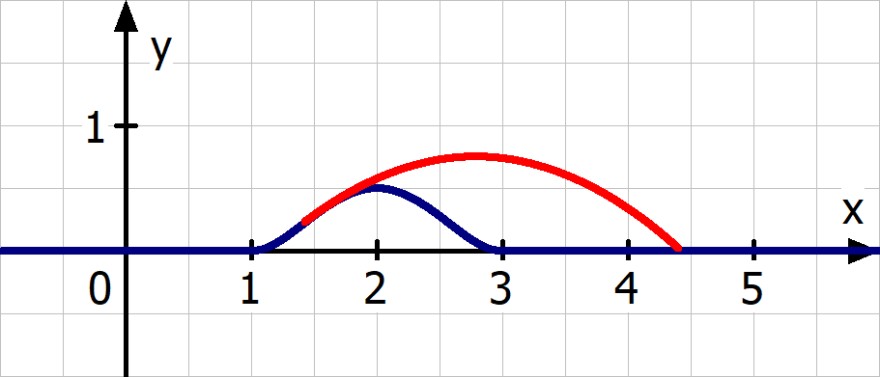
1. Der Ball wird modellhaft als punktförmig angenommen. Bei einem festen Schlag hebt er am Punkt P(1,42 |f(1,42)) von der Bahn ab. Seine Flugbahn ab dem Punkt P kann näherungsweise durch die Parabel q mit q(x) = - 0,28x2+ 1,56x - 1,42 beschrieben werden. Zeige, dass der Ball nicht direkt im Loch bei x = 5 landet.
q(x) = 0 --> x = 4.425 m
Der Ball landet ca. 57 cm vor dem Loch.
2. Berechne den Winkel, unter dem der Ball auf die Bahn trifft.
arctan(q'(4.425)) = -42.55°
Der Ball landet unter einem Winkel von ca. 42.55°
3. Das Hindernis soll auf einer Seite verkleidet werden. Die Kosten der Verkleidung betragen pro Quadratmeter 40€. Berechne die Kosten für die Seitenverkleidung.
40·∫ (1 bis 3) (0.5·x^4 - 4·x^3 + 11·x^2 - 12·x + 4.5) dx = 21.33 €
Skizze