Aufgabe:
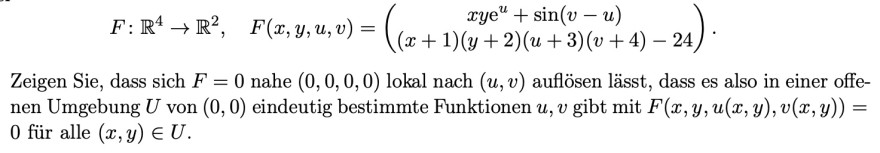
Problem/Ansatz:
Wir müssen zeigen, ob f stetig differenzierbar ist (klar). Dann, ob f in (x0, y0, u0, v0) eine Nullstelle ⇔ f(x0, y0) = 0. Dann Ist Dyf(x0, y0) invertierbar d.h. det (Dyf(x0, y0)) =/ 0. Die Gleichung f(x0, y0) = 0 kann danach in einer Umgebung um (x0, y0) aufgelöst werden? Wir wissen bei der Aufgabe nicht weiter