Bestimmen Sie die Schwerpunktkoordinaten der Fläche unter der Kurve f(x)=1/2e^x
In den Grenzen \( a=2 \) und \( b=4).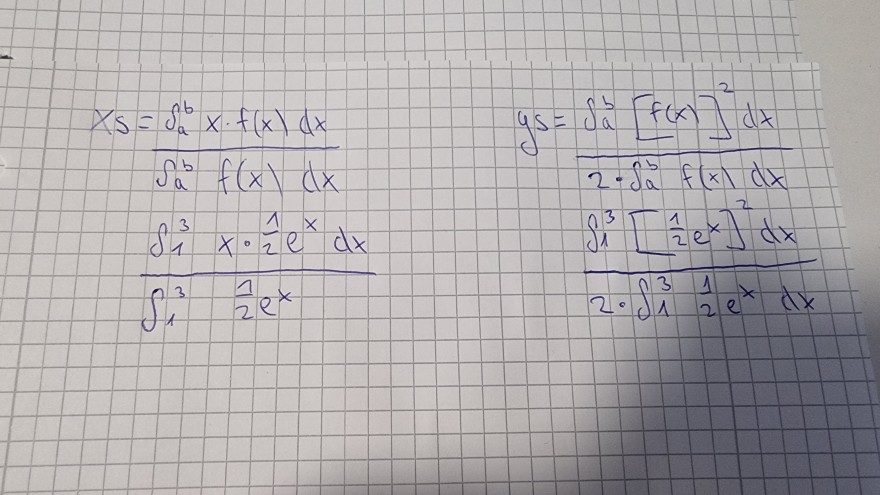
Text erkannt:
\( \begin{array}{l}X s=\frac{\int \limits_{a}^{b} x \cdot f(x) d x}{\int \limits_{a}^{b} f(x) d x} \\ y s=\frac{\int \limits_{a}^{b}[f(x)]^{2} d x}{2 \cdot \int \limits_{a}^{b} f(x) d x} \\ \frac{\int \limits_{1}^{3} x \cdot \frac{1}{2} e^{x} d x}{\int \limits_{1}^{3} \frac{1}{2} e^{x}} \\ \frac{\int \limits_{1}^{3}\left[\frac{1}{2} e^{x}\right]^{2} d x}{2 \cdot \int \limits_{1}^{3} \frac{1}{2} e^{x} d x} \\\end{array} \)