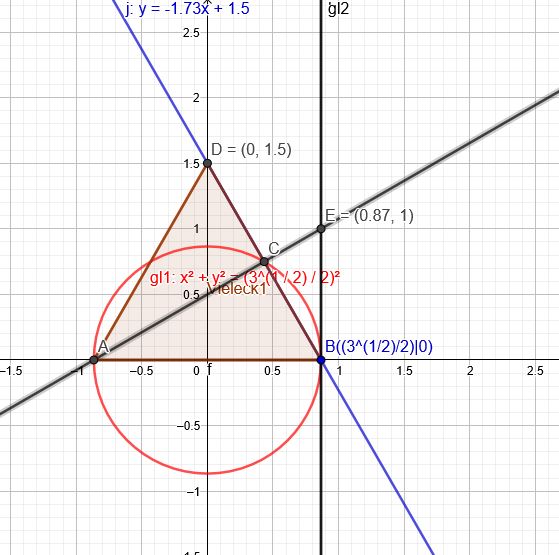
\( A(-\frac{\sqrt{3}}{2}|0) \) \( B(\frac{\sqrt{3}}{2}|0) \)
Gerade durch B mit \(m=- \sqrt{3} \)
\( \frac{y}{x-\frac{\sqrt{3}}{2}}=- \sqrt{3} \)
\( y=- \sqrt{3}*x +\frac{3}{2}\)
Kreis durch A und B mit \(r=\frac{\sqrt{3}}{2} \)
\(y= \sqrt{\frac{3}{4}-x^2} \)
Schnittpunkt C:
\( - \sqrt{3}*x +\frac{3}{2}=\sqrt{\frac{3}{4}-x^2} |^{2}\)
\( 3x^2 -3*\sqrt{3}*x+\frac{9}{4}=\frac{3}{4}-x^2 \)
\(4x^2 -3*\sqrt{3}*x=-\frac{3}{2} |:4 \)
\(x^2 -\frac{3}{4}*\sqrt{3}*x=-\frac{3}{8} \)
\((x-\frac{3}{8}*\sqrt{3})^2=-\frac{3}{8}+(\frac{3}{8}*\sqrt{3})^2=\frac{3}{64} | \sqrt{~~} \)
1.)
\(x-\frac{3}{8}*\sqrt{3}= \frac{1}{8}\sqrt{3} \)
\(x_1= \frac{1}{2}\sqrt{3} \) \( y_1=- \sqrt{3}* \frac{1}{2}\sqrt{3} +\frac{3}{2}=0\) →kommt nicht in Betracht.
2.)
\(x-\frac{3}{8}*\sqrt{3}= -\frac{1}{8}\sqrt{3} \)
\(x_2= \frac{1}{4}*\sqrt{3} \) \( y_2=- \sqrt{3}*\frac{1}{4}*\sqrt{3} +\frac{3}{2}=\frac{3}{4}\)
\(C( \frac{1}{4}*\sqrt{3}|\frac{3}{4})\)
Gerade durch \( A(-\frac{\sqrt{3}}{2}|0) \) und \(C( \frac{1}{4}*\sqrt{3}|\frac{3}{4})\)
\( \frac{y}{x+\frac{1}{2}\sqrt{3}}=\frac{1}{3}\sqrt{3} \) geschnitten mit \(x= \frac{1}{2}\sqrt{3} \)
\( \frac{y}{ \frac{1}{2}\sqrt{3}+\frac{1}{2}\sqrt{3}}=\frac{1}{3}\sqrt{3} \)
\(y=1\)
\(E(\frac{1}{3}\sqrt{3}|1)\)