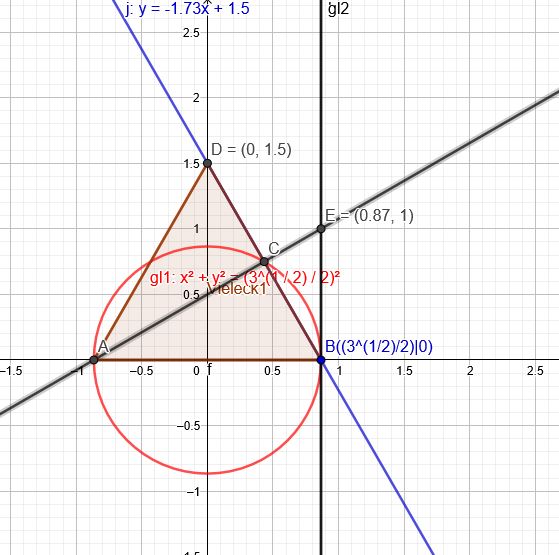
A(−23∣0) B(23∣0)
Gerade durch B mit m=−3
x−23y=−3
y=−3∗x+23
Kreis durch A und B mit r=23
y=43−x2
Schnittpunkt C:
−3∗x+23=43−x2∣2
3x2−3∗3∗x+49=43−x2
4x2−3∗3∗x=−23∣ : 4
x2−43∗3∗x=−83
(x−83∗3)2=−83+(83∗3)2=643∣
1.)
x−83∗3=813
x1=213 y1=−3∗213+23=0 →kommt nicht in Betracht.
2.)
x−83∗3=−813
x2=41∗3 y2=−3∗41∗3+23=43
C(41∗3∣43)
Gerade durch A(−23∣0) und C(41∗3∣43)
x+213y=313 geschnitten mit x=213
213+213y=313
y=1
E(313∣1)