Aufgabe:
Bestimmen Sie die folgenden Integrale
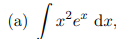
Text erkannt:
(a) \( \int x^{2} e^{x} \mathrm{~d} x \),
Problem/Ansatz:
Hier die Lösung zu der Aufgabe:
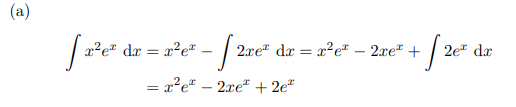
Text erkannt:
(a)
\( \begin{aligned} \int x^{2} e^{x} \mathrm{~d} x & =x^{2} e^{x}-\int 2 x e^{x} \mathrm{~d} x=x^{2} e^{x}-2 x e^{x}+\int 2 e^{x} \mathrm{~d} x \\ & =x^{2} e^{x}-2 x e^{x}+2 e^{x} \end{aligned} \)
Meine Frage ist, wie das + zustande kommt. Ich komme einfach nicht drauf. Also:
Ich habe zunächst [ex*x2] - ∫2x*ex dx. Soweit so klar. Jetzt habe ich für ∫2x*ex dx f´(x)= ex , g(x)=2x, f(x)=ex und g´(x)=2. Also: [ex*x2] (schreibe ich ab) - [2x* ex] - ∫ 2*ex . Woher kommt denn hier das + laut Lösung? Hätte ich -2*ex gehabt ok, und dann - - , aber so verstehe ich nicht vorher das + kommt. Kann mir das vielleicht einer erläutern?