Text erkannt:
Aufgabe 3
Bestimmen Sie sämtliche lokalen Extremstellen der Funktion
\( f(x, y)=\left(1-x^{2}\right) \cdot y \)
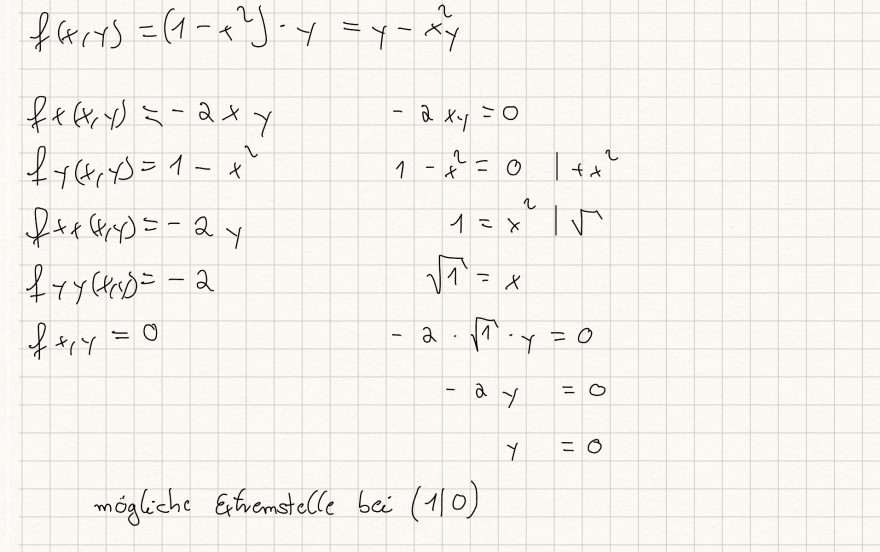
Text erkannt:
\( \begin{array}{l} f(x, y)=\left(1-x^{2}\right) \cdot y=y-x^{2} y \\ f x(x, y)=-2 x y \quad-2 x y=0 \\ f_{y}(x, y)=1-x^{2} \quad 1-x^{2}=0 \mid+x^{2} \\ f+x(x, y)=-2 y \\ 1=x^{2} \mid \sqrt{ } \\ f_{7} y(x, y)=-2 \\ \sqrt{1}=x \\ f x, y=0 \\ -2 \cdot \sqrt{1} \cdot y=0 \\ -2 y=0 \\ y=0 \\ \end{array} \)
mögliche Etremstelle bei (1|0)
Hallo, habe ich bis hierhin richtig gerechnet? Der nächste Schritt wäre die Hesse Matrix oder bin ich auf dem falschen Weg?