Wie kommt man auf diese Umformung?

Question

Aufgabe:

Ich soll mithilfe der vollständigen Induktion zeigen ,dass folgende Formel für alle n aus den natürlichen Zahlen gilt:

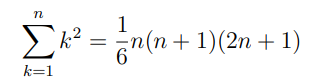
Text erkannt:

\( \sum \limits_{k=1}^{n} k^{2}=\frac{1}{6} n(n+1)(2 n+1) \)

Problem/Ansatz:

Ich verstehe nicht wie man auf dem gelb markierten Teil umformt. Wieso steht 1/6n plötzlich in der Klammer und was passiert mit (n+1)^2 (rot markiert)?

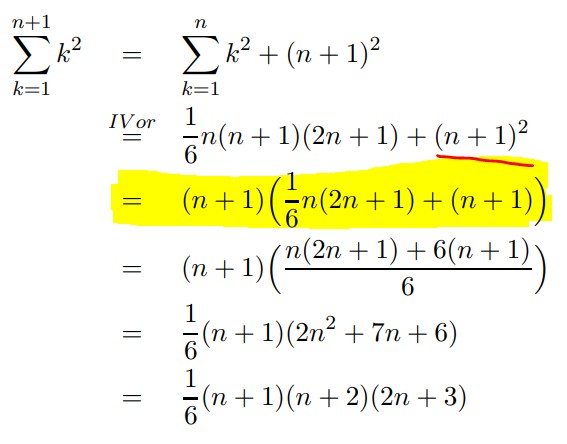
Text erkannt:

\( \begin{aligned} \sum \limits_{k=1}^{n+1} k^{2} & =\sum \limits_{k=1}^{n} k^{2}+(n+1)^{2} \\ & \stackrel{\text { IVor }}{=} \frac{1}{6} n(n+1)(2 n+1)+\left(\underline{(n+1)^{2}}\right. \\ & =(n+1)\left(\frac{1}{6} n(2 n+1)+(n+1)\right) \\ & =(n+1)\left(\frac{n(2 n+1)+6(n+1)}{6}\right) \\ & =\frac{1}{6}(n+1)\left(2 n^{2}+7 n+6\right) \\ & =\frac{1}{6}(n+1)(n+2)(2 n+3)\end{aligned} \)

Comments

Hallo,

beachte die rot markierten Terme.

\( \begin{aligned} \sum \limits_{k=1}^{n+1} k^{2} & =\sum \limits_{k=1}^{n} k^{2}+(n+1)^{2} \\ & \stackrel{\text { IVor }}{=} \frac{1}{6} n\red{(n+1)}(2 n+1)+\red{(n+1)}(n+1) \\ & =\red{(n+1)}\left(\frac{1}{6} n(2 n+1)+(n+1)\right) \\ & =(n+1)\left(\frac{n(2 n+1)+6(n+1)}{6}\right) \\ & =\frac{1}{6}(n+1)\left(2 n^{2}+7 n+6\right) \\ & =\frac{1}{6}(n+1)(n+2)(2 n+3)\end{aligned} \)

---

Das macht jetzt Sinn für mich, vielen Dank für den ausführlichen Lösungsweg!

Answer 1

Wie es aussieht, wurde \((n+1)\) ausgeklammert.

Comments

Ok, dankeschön!

Answer 2

Es wurde (n+1) ausgeklammert.

Wenn du aus (n+1)^2  den Term (n+1) ausklammerst, bleibt (n+1) in der Klammer zurück.

Comments

Danke für die Antwort!