Hallo,
A) Trennung der Variablen:
yy'=x ; y'=dy/dx
y *dy/dx =x → alles mit y auf eine Seite bringen, alles mit x auf die andere Seite bringen.
y dy= x dx ->beide Seiten integrieren
y^2/2 = x^2/2 +C | *2
y^2 =x^2 +2C
y= ± √(x^2 +2C)
B) Trennung der Variablen:
y' + x^2 y = 5x^2
y'= 5x^2 -x^2 y
y'=x^2 (5-y)

C) Trennung der Variablen:
y' = -2xy + 2xy^2
y'= -2x(y-y^2)
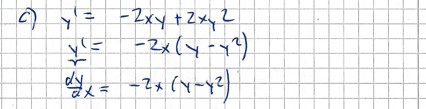


D) Ansatz y=e^kx
2 Mal ableiten und in die DGL einsetzen
y'' - 6y' + 9y = e^x
->Charakt. Gleichung:
k^2 -6k +9=0
k1,2= 3
yh=(C1 x+C2) e^(3x)
yp=A e^x ->2 Mal ableiten
yp'= A e^x
yp''=A e^x
y, yp'. yp'' in die DGL einsetzen:
A e^x- 6 A e^x + 9A e^x = e^x
4 A e^x= e^x | e^x≠ 0
4 A = 1
A=1/4
yp= A e^x
yp=e^x/4
y=yh +yp