Ungleichung; Werte; und/oder

Question

Aufgabe:

die Aufgabe |5x-20|>3x+15 hat die Lösung(en) bzw. den Lösungsbereich für x>35/2 ∨ x<5/8 (∨=oder).

Die Aufgabe 3x+15>|5x-20| hat die Lösung(en) bzw. den Lösungsbereich für x>5/8 ∧ x<35/2 (∧=und)

Meine Frage: Wie stellt man fest , wann beide Bedingungen gleichzeitig erfüllt sein müssen (∧) und wann nur eine (∨)?

Danke im Voraus und LG

Answer 1

Hallo

x>35/2 kann ja gar nicht  auch x<5/8 sein d.h. x biet im Bereich (-oo,5/8) oder im Bereich (35/2,oo) die Bereiche haben nichts gemeinsam

dagegen x>5/8  würde  allein den Bereich (5/8,oo) x<35/2 den Bereich (-oo,35/2 umfassen , das geht nicht beides zusammen hat man also den Bereich (5/8,35/2)

also sieht man nach welche x auf dem Zahlenstrahl möglich sind, am einfachsten sieht man das wenn man die 2 Seiten als Graphen von Funktionen zeichnet, rot 3x+15 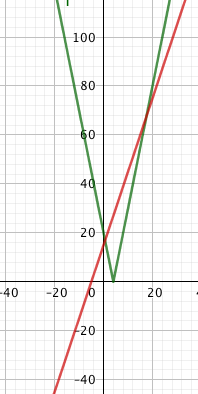  grün |5x-20|

Gruß lul

Answer 2

|5x-20|>3x

1. x>= 4

5x-20> 3x+15

2x> 35

x> 17,5

2. x<4

-5x+20 >3x+15

8x < 5

x < 5/8

x< 0,625

L = (-oo; 0,625) ∪ (17,5; +oo) = R \[0,625; 17,5]