Hallo,
Ich vereinfache das Modell zunächst so, dass es nur aus zwei Seilabschnitten besteht. Den Recker lasse ich weg, aber das Gewicht der Schäkel berücksichtige ich. Der Dyneemavorlauf besteht aus Polyethylen und das hat in etwa die Dichte von Wasser. D.h. es ist im Wasser fast schwerelos. Deshalb betrachte ich den Vorlauf als gestrecktes Seil ohne Durchhang.
Bleiben eine Gerade (der Vorlauf), das Gewicht der Schäkel und der nach Kettenlinie durchhängende Draht.
Zunächst mal die Theorie: eine Kettenlinie kann man durch die Funktion$$f\left(x\right)=a\cosh\left(\frac{x-x_{0}}{a}\right)+y_{0}$$beschreiben. \(f(x)\) gibt die Höhe der Kette in Abhängigkeit der horizontalen Entfernung \(x\) eines gewählten Nullpunkts. \(a\), \(x_0\) und \(y_0\) sind Längen. \(x_0\) ist die Koordinate mit dem größten Durchhang und mit \(y_0\) kann man die Kette in der Höhe verschieben.
Um den Bezug zur Länge der Kette herzustellen, gilt es diese zu berechnen. Für jede (normale!) Funktion ist die Länge \(L\) der Kurve zwischen zwei Koordinaten \(x_1\) und \(x_2\)$$L=\int\limits_{x_1}^{x_2}\sqrt{1+(f'(x))^2}\,\text{d}x$$und die Ableitung \(f'\) der Kettenlinie ist$$f'\left(x\right)=\sinh\left(\frac{x-x_{0}}{a}\right)$$Daraus folgt dann$$L=\int\limits_{x_1}^{x_2}\sqrt{1+(f'(x))^2}\,\text{d}x = \int\limits_{x_1}^{x_2}\cosh\left(\frac{x-x_{0}}{a}\right)\,\text{d}x \\ \phantom{L}= \left.a\sinh\left(\frac{x-x_{0}}{a}\right)\right|_{x_1}^{x_2}\\ \phantom{L}= a\left(\sinh\left(\frac{x_{2}-x_{0}}{a}\right)-\sinh\left(\frac{x_{1}-x_{0}}{a}\right)\right)\\ \phantom{L}= a\left(f'(x_2)-f'(x_1)\right)\\$$Und das macht die Sache relativ einfach. Einfach deshalb, weil in diesem Fall die Kräfte am Seil gegeben sind (Gewicht und Zug). Dazu sieht man sich die Kraftdreiecke an den Kettenenden an:
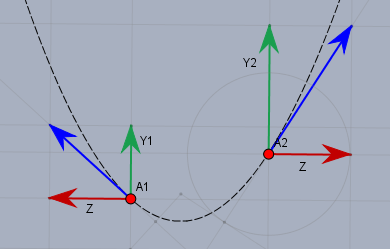
Die roten Pfeile \(Z\) links und rechts bilden die Zugkraft und sind zwangsläufig gleich (solange man den Fahrtwiderstand im Wasser vernachlässigt). Damit das Kräftegleichgewicht in der Vertikalen passt, muss die Summe der senkrechten Komponenten (grün) gleich dem Gewicht \(G\) des Seils sein.$$Y_1 + Y_2 = G$$Nun gilt aber auch noch$$f'(x_1) = -\frac{Y_1}{Z} \quad f'(x_2)=\frac{Y_2}{Z}$$Und daraus folgt:$$f'(x_2)-f'(x_1) = \frac{Y_2}{Z} + \frac{Y_1}{Z} = \frac{G}{Z} \\ \implies L = a\cdot \frac{G}{Z} \implies a = \frac{L\cdot Z}{G}$$und die drei Größen auf der rechten Seite sind alle vorgegeben. Damit ist das \(a\) bekannt!
Jetzt brauchen wir noch die Betrachtung der zusätzliche Last \(S\) durch die Schäkel. Ist \(f_l\) die Funktion der linken Kette von \(l_1\) bis \(l_2\) und \(f_r\) die Funktion der rechten Kette am Schäkel von \(r_1\) bis \(r_2\), so gibt sich am Aufhängepunkt eines Gewichts \(S\) folgendes Bild.
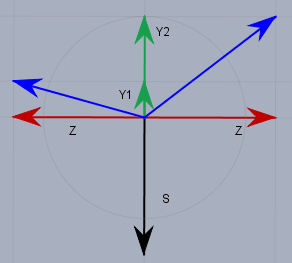
Die blauen Kräfte bilden die Seilkräfte, die in die waagerechte Komponente \(Z\) (den Zuganteilm, rot) und in die beiden senkrechten Komponenten \(Y_1\) und \(Y_2\) (grün) aufgeteilt sind. Auf Grund des Kräftegleichgewichts in vertikaler Richtung gilt$$S = Y_1 +Y_2$$ und genau wie oben ist$$f_l'(l_2) = -\frac{Y_1}{Z} \quad f_r'(r_1)=\frac{Y_2}{Z} \quad \text{mit} \space l_2=r_1$$ und daraus folgt$$f'_{r}(r_1) - f'_{l}(l_2) = \frac{S}{Z} \quad\implies f'_r(r_1) = f'_l(l_2)+ \frac{S}{Z}$$Jetzt wird's ein bißchen länglich - ich verzichte mal auf Details. Man startet mit einer Schätzung für die Anfangssteigung \(f'_0\) des Seils beim Havaristen. Hier soll die Position \(x=0\) sein. Aus der Länge des Dyneemavorlaufs kann ich daraus die Position des Schäkels berechnen$$x_S = \frac{l_{1}}{\sqrt{1+{f'_0}^2}}, \quad y_S = \frac{f'_0 l_{1}}{\sqrt{1+{f'_0}^2}} + h_1$$ Und aus der Anfangssteigung \(f'_0\) und dem Verhältnis \(S/Z\) die Anfangssteigung \(f'_1\) des Drahtseils $$f'_1 = f'_0+\frac{S}{Z}$$ Die Konstante \(a\) für die Kettenfunktion des Drahtseils habe ich oben schon erklärt$$a= \frac{l_2 \cdot Z}{G_S}$$und daraus kann man dann das \(x_0\) für die Kettenfunktion des Drahtseils berechnen$$\begin{aligned} f'_1&= f'\left(x_S\right)=\sinh\left(\frac{x-x_{0}}{a}\right)\\ \implies x_0 &= x_S - a\operatorname{arcsinh}\left(f'_1\right) \\ &= \frac{l_{1}}{\sqrt{1+{f'_0}^2}} - \frac{l_2 \cdot Z}{G_S}\operatorname{arcsinh}\left(f'_0+\frac{S}{Z}\right)\\ \end{aligned}$$Und aus der Formel für die Seillänge (s.o.) folgt dann das \(x_2\) - d.h. die X-Position des Drahtseilendes$$l_2= a\left(f'(x_2)-f'_1\right) \implies f'(x_2) = \frac{l_2}{a} +f'_1 = f'_1 + \frac{G_S}{Z}\\ f'(x_2)=\sinh\left(\frac{x_2-x_{0}}{a}\right) \implies x_2 = a\operatorname{arcsinh}\left(f'(x_2)\right)+x_0$$Und damit berechnet man die Höhe \(h_2^*\) des Drahtseilendes$$\begin{aligned} h_2^* &= a\cosh\left(\frac{x_2-x_0}{a}\right) + y_0 \\ &= a\cosh\left(\operatorname{arcsinh}\left(f'(x_2)\right)\right) + y_0 \end{aligned}$$Das \(y_0\) erhält man aus dem Drahtseilanfang bei \((x_S,\,y_S)\)$$y_S = a\cosh\left(\frac{x_S-x_0}{a}\right) + y_0 \\ \implies y_0 = y_S - a\cosh\left(\frac{x_S-x_0}{a}\right) $$Was haben wir nun gewonnen? Wir haben einen Algorithmus, der aus einer Steigung \(f'_0\) am Anfang die Höhe des Seils am Ende berechnet - bei vorgegebener Zugkraft \(Z\). Da die Höhe \(h_2\) am Ende bekannt ist (Aufhängepunkt am Schlepper), kann über Variation von \(f'_0\) der Seilverlauf nummerisch berechnet werden. Der tiefste Durchhang ist an der Position \(x_0\).
Bei Z=5t komme ich auf einen Durchhang von 5,7m unter der Wasserlinie. Dabei befindet sich der Dyneemavorlauf aber fast vollständig außerhalb des Wassers, d.h. die ursprüngliche Annahme der 'Schwerelosigkeit' passt nicht! Bei Z=2t berechne ich aber bereits einen Durchhang von 27,4m unter der Wasserlinie, wie man hier sieht
Wenn Du unten rechts auf das Bild klickst, öffnet sich die Desmos-Seite. Oben rechts kannst Du dann die Zugkraft einstellen und dann musst Du den Schieber bei \(f_{s0}= \dots\) so einstellen, dass das Seilende rechts wieder durch den Aufhängepunkt bei \(h=5\,\text{m}\) geht. Der Durchhang wird dann angezeigt.
Gruß Werner
PS.: freue mich über jedes Feedback ;-)