Bestimmen Sie die Gleichung der Tangente t.

Question

Aufgabe:

Der Graph von f(x) = 0,05 x3 + 0,25 x2 − 0,2x + 1 und die
Tangente t von f im Kurvenpunkt P(−5|2) schließen eine
Fläche A ein.
a) Bestimmen Sie die Gleichung der Tangente t.
b) Begründen Sie zunächst durch inhaltliche Überlegun-
gen, warum der Graph von f und die Tangente t neben
P einen weiteren Schnittpunkt besitzen.
c) Bestimmen Sie mit dem TR/Computer den Inhalt der
Fläche A, welche vom Graphen von f und der Tangente
t eingeschlossen wird.

Problem/Ansatz:

Wie finde ich heraus was t(x) ist?

Danke!

Answer 1

Funktion und Ableitung

f(x) = 0.05·x^3 + 0.25·x^2 - 0.2·x + 1
f'(x) = 0.15·x^2 + 0.5·x - 0.2

Tangente an der Stelle a = -5

a = -5
f(a) = 2
f'(a) = 1.05

t(x) = 1.05·(x + 5) + 2 = 1.05·x + 7.25

Differenzfunktion

d(x) = f(x) - t(x) = 0.05·x^3 + 0.25·x^2 - 1.25·x - 6.25

Schnittstellen von f und t. Nullstellen der Differenzfunktion

d(x) = 0 --> x = -5 ∨ x = 5

Fläche

A = ∫ (-5 bis 5) d(x) dx = - 125/3

Der Flächeninhalt beträgt 125/3 = 41.67 FE

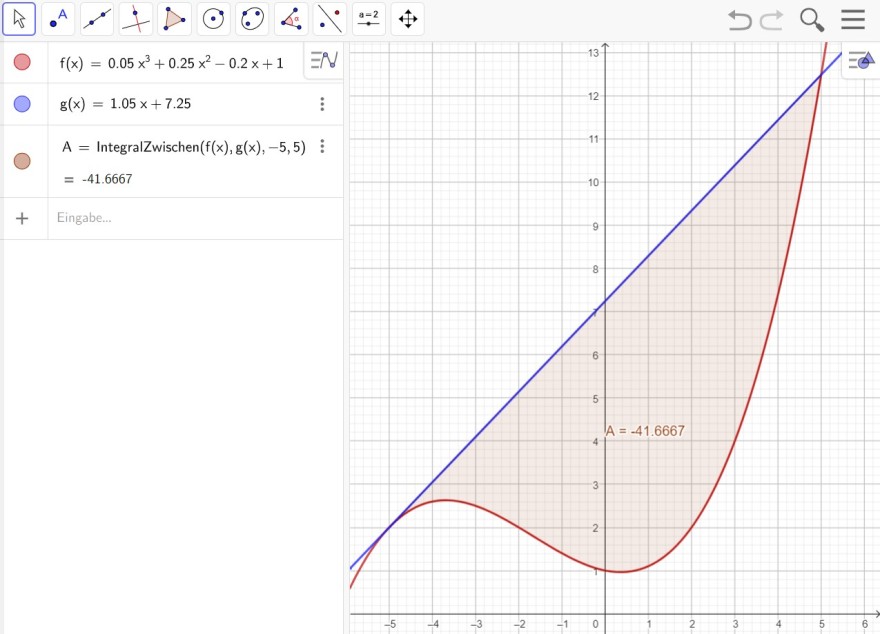
Fläche mit Geogebra

Answer 2

t hat die Steigung f '(-5) und geht durch (-5;2).

Answer 3

t(x) = (x+5)* f '(-5) +f(-5)