a)
Du könntest darauf eingehen, dass die Änderungsrate im Bereich von 5 bis 12 fast gleich bleibt, weil dort der Graph näherungsweise linear verläuft.
Evtl. kann man auch erahnen, dass der Graph um 5 uhr noch linksgekrümmt ist und gegen 16 Uhr sicher rechtsgekrümmt.
Du könntest daher hier näherungsweise, die Wendestelle angeben, an der du den stärksten Temperaturanstieg erwartest.
Rechnerisch kommst du da auf ca. 8.
b) Beantworten Sie mithilfe der Modellfunktion die folgenden Fragen: In welchem Bereich steigt die Temperatur, in welchem Bereich fällt sie?
f'(x) = 0 --> x = 0 ∨ x = 140/9 ≈ 15.56 ≈ 15:33 Uhr
Zu welchem Zeitpunkt ist die momentane Anderungsrate am größten, wie groß ist sie?
f''(x) = 0 --> x = 70/9 = 7:47 Uhr
f'(70/9) = 49/30 = 1.633 °C/h
Vergleichen Sie die Anderungsralen zu Beginn und Ende des angegebenen Bereichs.
f'(5) = 1.425 °C/h
f'(21) = - 3.087 °C/h
c) Wie könnte die Kurve vor 5 00 und nach 21.00 aussehen? Begründen Sie, dass die Modellfunktion für diese Bereiche nicht geeignet ist.
Wenn man davon ausgeht, das die Tiefsttemperatur in der Nach bei ca. 6 Grad liegt würde sich die Temperatur vor 5 von 10 Grad auf 12 Grad ansteigen und nach 21 Uhr von ca. 17 Grad auf 10 Grad abfallen.
Ich habe mal eine Skizze dafür gemacht
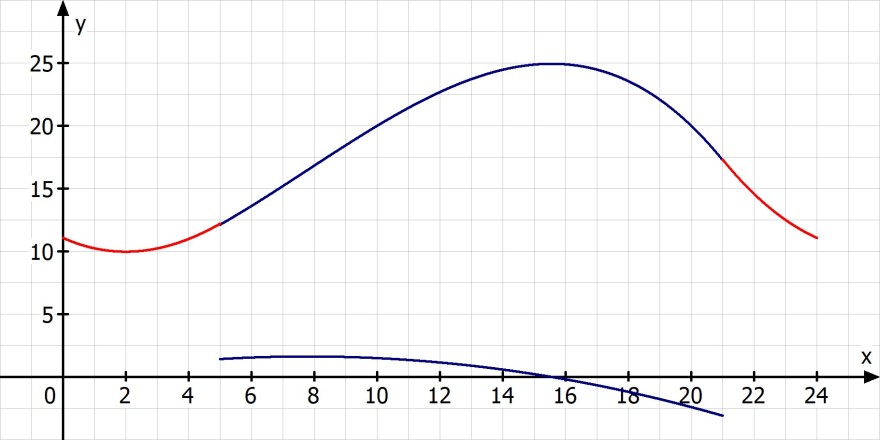
PS: Eingezeichnet habe ich auch noch die Änderungsrate der Funktion im Intervall von 5 bis 21 Uhr.