Aufgabe:
Problem/Ansatz:
hallo, mir ist unklar wie ich anhand der Aufgaben B und C sehe was das Supremum und infimum ist. 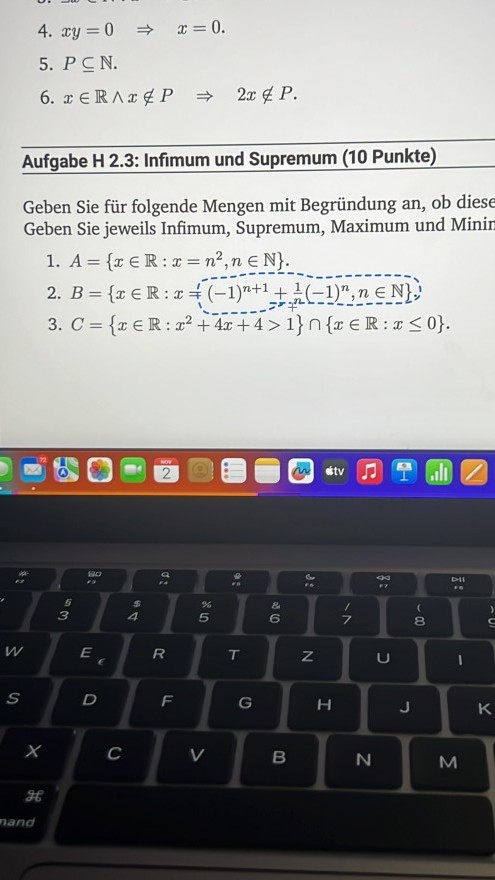
Text erkannt:
4. \( x y=0 \quad \Rightarrow \quad x=0 \).
5. \( P \subseteq \mathbb{N} \).
6. \( x \in \mathbb{R} \wedge x \notin P \quad \Rightarrow \quad 2 x \notin P \).
Aufgabe H 2.3: Infimum und Supremum (10 Punkte)
Geben Sie für folgende Mengen mit Begründung an, ob diese Geben Sie jeweils Infimum, Supremum, Maximum und Minin
1. \( A=\left\{x \in \mathbb{R}: x=n^{2}, n \in \mathbb{N}\right\} \).
2. \( B=\left\{x \in \mathbb{R}: x+\frac{1}{1}(-1)^{n+1}+\frac{1}{n}(-1)^{n}, n \in \mathbb{N}\right\} \);
3. \( C=\left\{x \in \mathbb{R}: x^{2}+4 x+4>1\right\} \cap\{x \in \mathbb{R}: x \leq 0\} \).