Aufgabe:
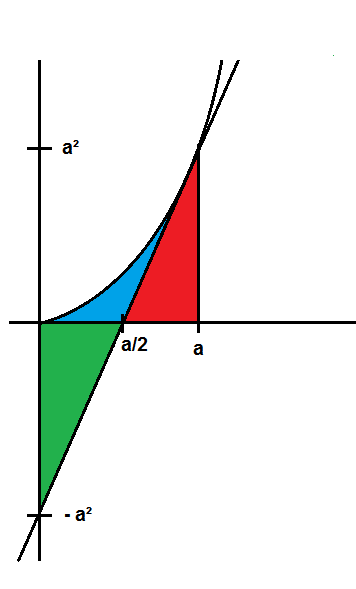
Beweisen Sie: Der Graph von f mit f(x) = x^{2}, die Tangente an f in P(a | f(a)) und die y-Achse begrenzen eine Fläche mit dem Inhalt A =$$\frac{1}{3}a^{3}$$
Folgenden Ansatz haben wir in der Schule gerechnet:
1. Tangenten Gleichung.
$$ t(x)=2ax*-a^{2}$$
2. Integral bilden:
$$ \int \limits_{0}^{a}(2ax-a^{2})-(x^{2})dx $$
Wenn man das dann auflöst kommt dann $$\frac{1}{3}a$$ raus.
Meiner Meinung nach ergibt das keinen Sinn, da man lediglich beweist, dass der Flächeninhalt der blauen und roten Fläche gleich $$\frac{1}{3}a$$ ist. Die rote und grüne Fläche ergeben ja zusammen 0.
Wo liegt da mein Denkfehler?