b) Bestimmen Sie den Inhalt der sichtbaren Frontfläche in \( \mathrm{m}^{2} \).
\( f(x)=0,0025 x^{3}-0,07 x^{2}+0,4 x+4 \)
\(A= \int\limits_{0}^{16}(0,0025 x^{3}-0,07 x^{2}+0,4 x+4)dx=[\frac{1}{4}\cdot0,0025x^4-\frac{1}{3}\cdot0,07x^3 +\frac{1}{2}\cdot0,4x^2+4x]=...)\)
Wie groß ist der Rauminhalt des Cafés?
\(V=A\cdot16[m^{3}] \)
c) Am Rand (Punkt A und Punkt D) sollen geradlinige Dachüberstände knickfrei angebaut werden. In welchem Winkel, gemessen zur Horizontalen, muss dies geschehen?
\( f(x)=0,0025 x^{3}-0,07 x^{2}+0,4 x+4 \)
\( f´(x)=0,0075 x^{2}-0,14 x+0,4 \)
\( f´(0)=0,4 \) Steigung \(m=tan(α)=0,4\) \( tan^(-1)(0.4)= 21,8°\)
\( f´(16)=... \)
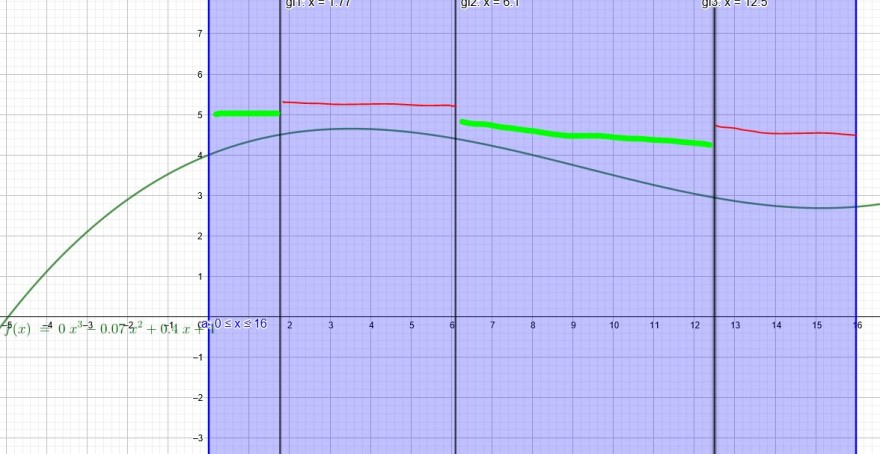
d) Das Dach soll mit Kunststoffplatten gedeckt werden, für die eine Mindestdachneigung von \( 10^{\circ} \) vorgesehen ist, damit das Regenwasser gut abläuft. Untersuchen Sie, ob diese Bedingung bei dem Dach weitestgehend erfüllt ist. Warum kann sie hier nicht an jeder Stelle erfüllt sein?
\( tan(10^{\circ})≈0,176 \)
\( 0,0075 x^{2}-0,14 x+0,4=0,176 \)
\(x_1=1,767\) bis hierhin kann das Dach belegt werden.
\( 0,0075 x^{2}-0,14 x+0,4=-0,176 \)
\( x_2=6,1 \)
\( x_3=12,5 \)
Von \(x_1=1,767\) bis \( x_2=6,1 \) ist das Dach zu flach
Von \( x_2=6,1 \) bis \( x_3=12,5 \) ist eine Belegung wieder möglich.