Aufgabe:
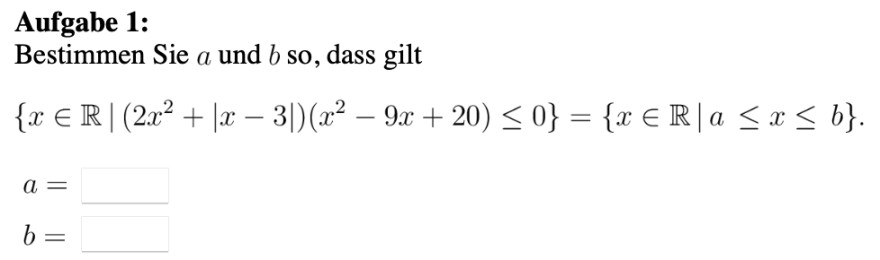
Text erkannt:
Aufgabe 1:
Bestimmen Sie \( a \) und \( b \) so, dass gilt
\( \begin{array}{l} \left\{x \in \mathbb{R} \mid\left(2 x^{2}+|x-3|\right)\left(x^{2}-9 x+20\right) \leq 0\right\}=\{x \in \mathbb{R} \mid a \leq x \leq b\} . \\ a= \\ b= \end{array} \)
Hallo Zusammen ich muss die Aufgabe 1 lösen und weiß nicht wie ich vorzugehen habe geschweige denn wie ich es zu lösen habe.