\(f(x)=a x^{3}+b x^{2}+c x+d\)
1.)
\(f(0)=1\)
\(f(0)=d\) → \(d=1\) → \(f(x)=a x^{3}+b x^{2}+c x+1\)
\(f(x)=a x^{3}+b x^{2}+c x+1\)
2.)
\(f(3)=1\) → \(f(3)=27a+9b+3c+1\) → \(27a+9b+3c+1=1\) →
→ \(27a+9b+3c=0\) → \(9a+3b+c=0\) → \(c=-9a-3b\)
\(f(x)=a x^{3}+b x^{2}+(-9a-3b) x+1\) →\(f(x)=a x^{3}+b x^{2}-(9a+3b) x+1\)
\(f´(x)=3a x^{2}+2b x-(9a+3b) \)
\(f´´(x)=6ax+2b \)
3.)
\(f´´(1)=-1\) → \(f´´(1)=6a+2b \) → \(6a+2b=-1 \) → \(2b=-1-6a \) → \(b=\frac{-1-6a }{2} \)→
→ \(b=-\frac{1+6a }{2} \) Einsetzen in \(c=-9a-3b\) : \(c=-9a-3\cdot(-\frac{1+6a }{2})\)→
→\(c=-9a+3\cdot(\frac{1+6a }{2})\) →\(c=-9a+\frac{3}{2}+9a\) →\(c=\frac{3}{2}\)
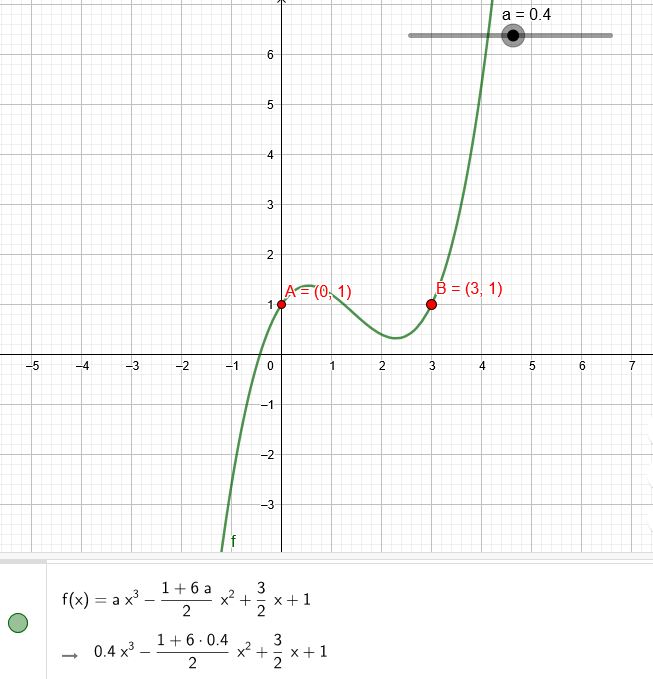
\(f(x)=a x^{3}-\frac{1+6a }{2} x^{2}+\frac{3}{2} x+1\)
Es fehlt noch eine Bedingung, damit \(a\) berechnet werden kann.