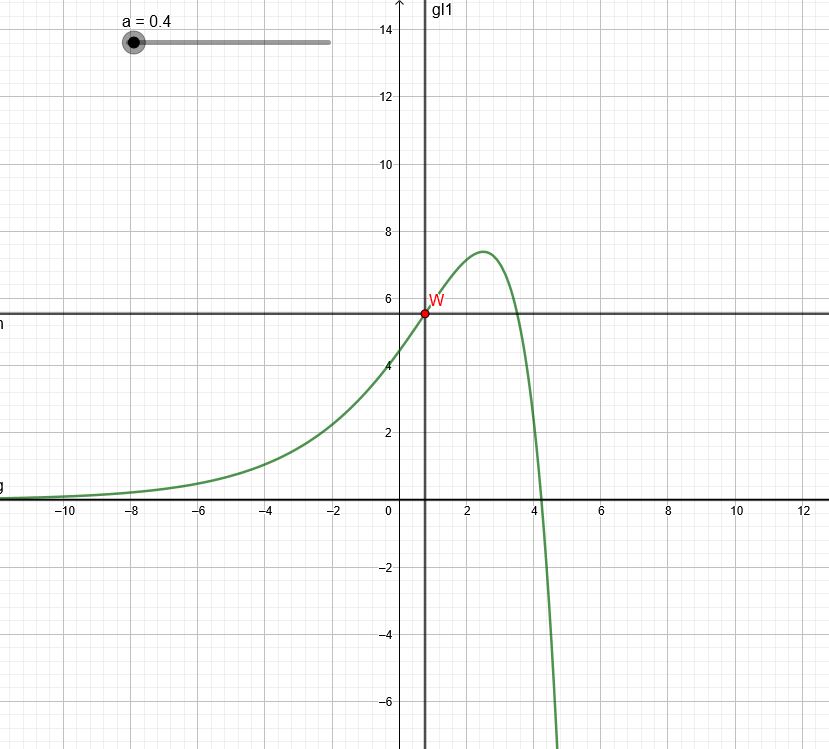
2. Berechnen Sie die Wendepunkte und die Ortskurve.
\(f_a(x)=(2e-e^{a·x}) \cdot e^{a·x}\\=2e\cdot e^{a·x}-e^{2ax}\)
\(f´_a(x)=2e \cdot a\cdot e^{a·x}-2a \cdot e^{2ax}\)
\(f´´_a(x)=2e \cdot a^{2}\cdot e^{a·x}-4a^2 \cdot e^{2ax}\)
\(2e \cdot a^{2}\cdot e^{a·x}-4a^2 \cdot e^{2ax}=0\)
\(e^{a·x}\cdot(2e \cdot a^{2}-4a^2 \cdot e^{ax})=0\)
\(e^{a·x}≠0\)
\(2e \cdot a^{2}-4a^2 \cdot e^{ax}=0 |:2a^2\) mit \(a≠0\)
\(e -2 \cdot e^{ax}=0 \)
\(e^{ax}=\frac{1}{2} e\)
\(ax\cdot lne =ln(\frac{1}{2} e)=1-ln(2)\) mit \(ln(e)=1\)
\(x =\frac{1-ln(2)}{a}\) \(f_a(\frac{1-ln(2)}{a})=(2e-e^{a·\frac{1-ln(2)}{a}}) \cdot e^{a·\frac{1-ln(2)}{a}}=(2e-e^{1-ln2}) \cdot e^{1-ln2}\)
\(W(\frac{1-ln(2)}{\red{a}}| (2e-e^{1-ln2}) \cdot e^{1-ln2}\)
Ortskurve:
Da \(\red{a}\) nur abhängig von der x-Stelle des Wendepunktes ist,
haben wir \(y= (2e-e^{1-ln2}) \cdot e^{1-ln2}\) als Ortskurve.