Sind die folgenden Polynome irreduzibel?

Question

Aufgabe:

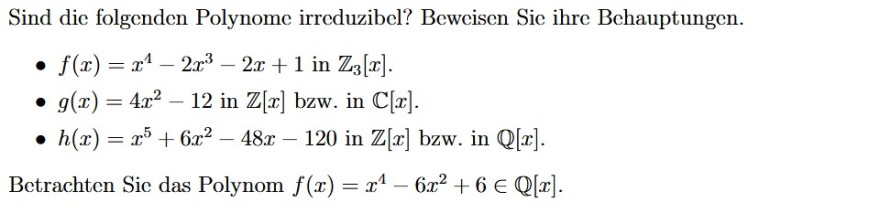
Text erkannt:

Sind die folgenden Polynome irreduzibel? Beweisen Sie ihre Behauptungen.
- \( f(x)=x^{4}-2 x^{3}-2 x+1 \) in \( \mathbb{Z}_{3}[x] \).
- \( g(x)=4 x^{2}-12 \) in \( \mathbb{Z}[x] \) bzw. in \( \mathbb{C}[x] \).
- \( h(x)=x^{5}+6 x^{2}-48 x-120 \) in \( \mathbb{Z}[x] \) bzw. in \( \mathbb{Q}[x] \).

Betrachten Sie das Polynom \( f(x)=x^{4}-6 x^{2}+6 \in \mathbb{Q}[x] \).

Problem/Ansatz:

Kann jemand meine Lösung überprüfen?

a) ist reduzibel denn, $$x^4-2x^3-2x+1=(x^2-x+1)(x^2+2x+1)$$ und die beiden sind element aus Z3.

b) $$4x^2-12=4(x^2-3)=(4(x-\sqrt{3})(x+\sqrt{3}))$$ Das ist sowohl reduzibel in Z als auch in C

c) Eisenstein liefert mit p=3 dass es Irreduzibel ist, in Q. Aber in Z habe ich keine Ahnung.

Answer 1

c) Jedes Polynom in ℤ[x] ist doch auch in ℚ[x].

Gäbe es also eine Zerlegung in ℤ[x] so wäre das doch auch eine in ℚ[x].

Also denke ich, dass es auch in ℤ[x] irreduzibel ist.