Der Lehrplan des Landes NRW für Mathematik in der Grundschule enthält der Begriff der Stukturorientierung. Dieser wird folgendermaßen präzisiert:
Bei strukturorientierten Aktivitäten und Betrachtungen wird in allen Bereichen des Faches das Regelhafte, Gesetzmäßige, Formelhafte der Erscheinungen sichtbar gemacht. Hierbei kommen Vorgehensweisen wie systematisch Variieren, Ordnen, Vergleichen, Verallgemeinern oder Übertragen zur Geltung.
Weiter heißt es:
Das Prinzip der Strukturorientierung unterstreicht, dass mathematische Aktivität häufig im Finden, Beschreiben und Begründen von Mustern besteht. Dazu werden die Gesetze und Beziehungen aufgedeckt, die Phänomene aus der Welt der Zahlen, der Formen und der Größen strukturieren. So werden auch Vorgehensweisen wie Ordnen, Verallgemeinern, Spezifizieren oder Übertragen entwickelt und geschult.
Anhand einer Aufgabe soll erläutert werden, wie die mathematische Aktivität des Findens von Mustern sowie des Beschreibens und Begründens von Mustern bei Grundschüler*innen angeregt werden kann:
Aufgabe:
a) Setze die unten dargestellte Folge dreieckiger Anordnungen von Chips um eine dreieckige Anordnung fort.
b) Kannst du auch ohne a) zu lösen, voraussagen, wie viele Chips die nächste bzw. die übernächste Anordnung enthält?

Die Frage zu Aufgabenteil b) zielt auf das Entdecken einer Gesetzmäßigkeit hinsichtlich der Anzahlen von Chips pro Dreieck.
Das in Aufgabe b) abgefragte Muster kann auf unterschiedliche Arten beschrieben werden. Eines davon wird nur von Schüler*innen entdeckt, die den Begriff der Quadratzahl bereits verinnerlicht haben. Grundsätzlich gilt für Musterentdeckungen und Beschreibungen, das die zentrale mathematische Tätigkeit des Rückgriffes auf Bekanntes gefordert ist.
Das Begründen des entdeckten Musters 'Quadratzahlenfolge' gelingt Grundschüler*innen nur dann, wenn der Begriff ‚Quadratzahl‘ mit dem Begriff ‚Quadrat‘ in Verbindung gebracht wird und auch dieser Begriff verinnerlicht wurde. Dann kann die Begründung durch das Umordnen der Darstellung

in die Darstellung
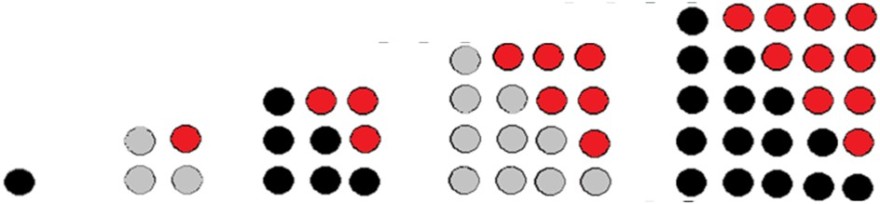
erfolgen.
Bei allen drei mathematischen Aktivitäten Finden, Beschreiben und Begründen von Mustern ist die die zentrale mathematische Tätigkeit des Rückgriffes auf Bekanntes gefordert.
Dies betonen auch die NRW-Mathematik-Richtlinien, in folgenden Passagen:
Schülerinnen und Schüler haben fachbezogene Kompetenzen ausgebildet,
- wenn sie zur Bewältigung einer Situation vorhandene Fähigkeiten nutzen, dabei auf vorhandenes Wissen zurückgreifen und sich benötigtes Wissen beschaffen,
- wenn sie die zentralen Fragestellungen eines Lerngebietes verstanden haben und angemessene Lösungswege wählen,
- wenn sie bei ihren Handlungen auf verfügbare Fertigkeiten zurückgreifen und ihre bisher gesammelten Erfahrungen in ihre Handlungen mit einbeziehen.
Allerdings bleiben Zusammenhänge zwischen Verstehen und Begriffserwerb sowie zwischen Rückgriff auf vorhandenes Wissen und Erkenntnisentwicklung zu wenig beleuchtet. Sie werden überstrahlt von den wieder und wieder angeführten Termini ‚Kompetenzen‘ und ‚Anwendungsorientierung‘.