Rechenweg Beweisaufgabe Bilinearform

Question

Meine Frage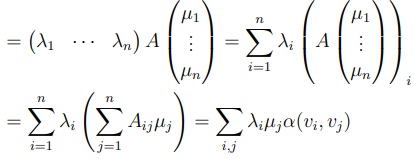

Text erkannt:

\( \begin{array}{l}=\left(\begin{array}{lll}\lambda_{1} & \cdots & \lambda_{n}\end{array}\right) A\left(\begin{array}{c}\mu_{1} \\ \vdots \\ \mu_{n}\end{array}\right)=\sum \limits_{i=1}^{n} \lambda_{i}\left(A\left(\begin{array}{c}\mu_{1} \\ \vdots \\ \mu_{n}\end{array}\right)\right)_{i} \\ =\sum \limits_{i=1}^{n} \lambda_{i}\left(\sum \limits_{j=1}^{n} A_{i j} \mu_{j}\right)=\sum \limits_{i, j} \lambda_{i} \mu_{j} \alpha\left(v_{i}, v_{j}\right)\end{array} \)

Hi an alle,

grundsätzlich geht es mir hier nur um die Frage wie man den Ausdruck von (Lambda 1 bis Lambda n) auf einmal als Summe über alle Lambdas i=1 bis n schreibt. Da Zeilenvektor mal Matrix ja wieder Zeilenvektor ergibt, schätze ich das der resultierende Zeilenvektor aufgespalten und als Summe dargestellt werden kann, ich komm von alleine aber im Moment leider nicht dahinter. Wäre sehr dankbar wenn jemand weiter weiß.

Answer 1

Dass da unten noch ein \(i\) als Index steht, siehst du aber, oder? Ansonsten betrachte den Vektor \(\vec{b}=A\vec{\mu}\) dann steht da \(\vec{\lambda}^T\cdot \vec{b}=\lambda_1 b_1 + \ldots +\lambda_n b_n\) (Skalarprodukt).