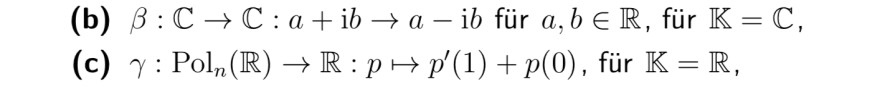
Text erkannt:
(b) \( \beta: \mathbb{C} \rightarrow \mathbb{C}: a+\mathrm{i} b \rightarrow a-\mathrm{i} b \) für \( a, b \in \mathbb{R} \), für \( \mathbb{K}=\mathbb{C} \),
(c) \( \gamma: \operatorname{Pol}_{n}(\mathbb{R}) \rightarrow \mathbb{R}: p \mapsto p^{\prime}(1)+p(0) \), für \( \mathbb{K}=\mathbb{R} \),
Aufgabe:
Hallo, bei folgenden 2 Aufgaben habe ich Schwierigkeiten die Linearität zu überprüfen. Bei Matrizen/Vektoren verstehe ich das aber bei solch komplexen Zahlen/Polynomen weiß ich nicht wie man vorgeht.
LG