Aufgabe:
Hallo, ich habe gestern angefangen Differentialgleichungen zu lernen, demnach hält sich mein allgemeines Verständnis noch in Grenzen. Nun habe ich versucht den homogenen Teil einer inhomogenen DGL (Störfunktion ist nicht mit angegebenen, homogener Teil in blau geschrieben) auf zwei Arten zu lösen. Allerdings unterscheidet sich das Ergebnis und ich finde meinen Fehler nicht. Das erste Ergebnis stimmt, das kam auch bei Wolfram Alpha raus. Vielleicht kann mir jemand helfen?
Gerne auch auf sonstige Fehler / Unstimmigkeiten hinweisen!
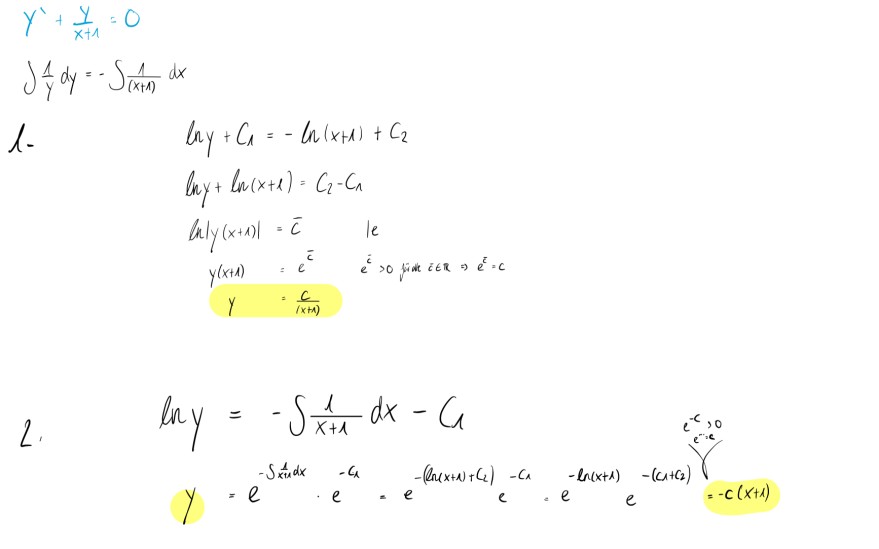
Text erkannt:
\( \begin{array}{l}\text { 2. } \ln y=-\int \frac{1}{x+1} d x-C_{1} \\ y=e^{-\int \limits_{x+1} d x} \cdot e^{-c_{1}}=e^{-\left(\ln (x+1)+c_{2}\right)} e^{-c_{1}}=e^{-\ln (x+1)} e^{-\left(c_{1}+c_{2}\right)}=-c(x+1) \\\end{array} \)