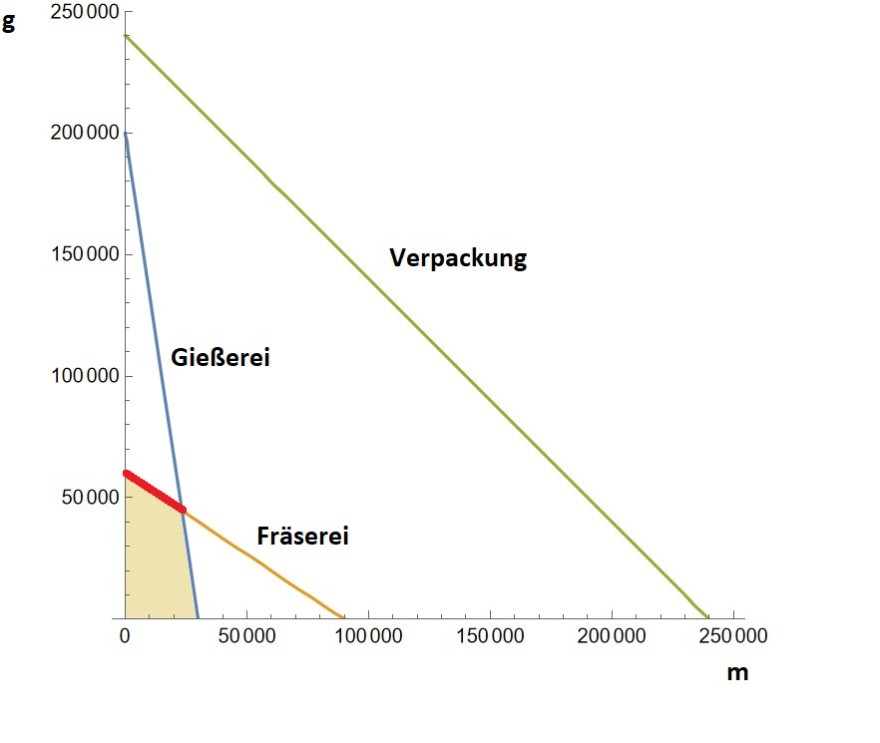
Die Verpackungsmaschine ist kein Engpass, das Polygon der Nebenbedingungen (im Bild hellbraun dargestellt) hat also 4 Ecken wobei dann noch der Ursprung wegfällt weil ohne Produktion kein Deckungsbeitrag entsteht.
Es bleiben somit als mögliches Optimum:
DB(m = 23333.3, g = 44444.4) = 36000
DB(m = 30000, g = 0) = 12000
DB(m = 0, g = 60000) = 36000
Wolfram Mathematica hat einmal das eine und einmal das andere gefunden.
Keine Ahnung, warum hier nicht.
Die Gerade der maximalen Fräserei-Kapazität hat dieselbe Steigung wie die Zielfunktion. Das Optimum liegt also nicht zwangsläufig in einer Ecke. Es gilt daher beispielsweise auch
DB(m = 15000, g = 50000) = 36000
Das Optimum ist nicht ein Punkt sonderrn eine Kante des Polygons der Nebenbedingungen, im Bild rot dargestellt: