Stetigkeit überprüfen

Question

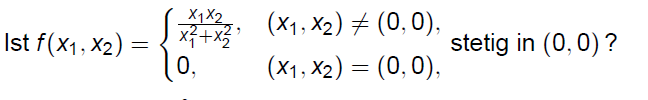
Text erkannt:

Ist \( f\left(x_{1}, x_{2}\right)=\left\{\begin{array}{ll}\frac{x_{1} x_{2}}{x_{1}^{2}+x_{2}^{2}}, & \left(x_{1}, x_{2}\right) \neq(0,0), \\ 0, & \left(x_{1}, x_{2}\right)=(0,0),\end{array}\right. \) stetig in \( (0,0) ? \)

Ich würde das Epsilon Delta Kriterium anwenden.

Also x_0= (0,0), demnach ||x-x_0||= \( \sqrt{x_1^2+x_2^2} \) <δ. Das gilt. ||f(x1,x2)-f(x_0)|| = |f(x1,x2)|. Die Norm wird nun zum Betrag. Wie kann ich es nun gut mit δ abschätzen? Evtl. Cauchy Schwarz?

Comments

Berechne \(f\) für den Fall \(x_1=x_2\) und für den Fall \(x_1=-x_2\). Und lass \(x_2\) in beiden Fällen gegen 0 gehen.

---

Eins reicht, weil f(0,0)=0 festgelegt ist.

Answer 1

Warum so kompliziert? Probiere ein paar Nullfolgen in \(\R^2\) aus und dazu die Funktionswerte. Wogegen (wenn überhaupt) konvergieren die Funktionswerte?

Dann kommst Du sehr schnell darauf, dass \(f\) in \((0,0)\) nicht stetig ist.

Comments

Ok, kann man auch links bzw. die rechtstetigkeit überprüfen und dann auf beidseitige Stetigkeit schließen, wenn die Bedingungen wahr sind, oder geht dies im Mehrdimensionalen nicht?

---

Du willst es immer noch kompliziert? Es gibt kein links und rechts. Welche Folgen hast Du ausprobiert?

---

ja ich hab jetzt die Folge "1/n" genommen und komm auf den Schluss das die Funktion nicht stetig ist. Nur noch eine Frage bezüglich der Anwendbarkeit der Definition. Also allgemein ist die Definition von Stetigkeit ja: f heißt an Stelle x_o stetig falls lim x→ x_o f(x) existiert und dieser Grenzwert =f(x_o). Kann man im Mehrdimensionalen auch mit dieser Definition arbeiten, oder bietet sich hier eher das Folgenkriterium eher an?

---

1/n ist keine Folge in \(\R^2\).

Die Def. in \(\R\) und in \(\R^2\) ist genau die gleiche. Und das was Du nennst, ist die Def. über Folgen (die andere wäre die mit \(\varepsilon-\delta\)).

Also, welche Folgen in \(\R^2\) hast Du genommen, mit welchem Ergebnis? Bitte genaue Angaben (möchte sicherstellen, dass Du es richtig angewandt hast).

---

Also ich habe gemeint lim n→∞ (1/n, 1/n) = (0,0) (hätte mich genauer ausdrücken sollen). Also haben wir unsere Nullfolge, jetzt setzen wir ein in unsere Funktion ein: lim n→∞ (1/n*1/n)/((1/n)^2)*(1/n)^2)) = 1/2. Jedoch ist f(0,0)≠1/2. Also ist die Funktion nicht stetig

---

Gut. Auch gut aufgeschrieben. Schreib aber explizit \(\lim f(\frac1n,\frac1n)=\lim ... =\frac12\neq f(0,0)\), damit der Bezug zur Folgenstetigkeit klar wird.

Du hast nun also Stetigkeit mit Angabe einer einzigen Folge widerlegt.

Wenn Du weiterdenken magst: Widerlege die stetige Ergänzbarkeit in (0,0). Dazu brauchst Du eine zweite Folge.

---

Ok ich werds mal versuchen. Aber nur noch eine kleine Frage. Könnte man es auch mit der allgemeinen Definition hier so anschreiben: lim (x1,x2)→(0,0) f(x1,x2) = f(0,0). Ich mein hier würde mir diese Definition nicht viel bringen, aber wäre die Schreibweise korrekt oder unüblich

---

Ja, das wäre die Bedingung für Stetigkeit in (0,0). Ist auch dasselbe, was Du oben als allg. Def. geschrieben hast (mit x->x_o).

---

Ok vielen Dank