No Hilfe bei b)
Der Planungsbeauftragte, Herr Meiners, mag keine Kreisverkehre und möchte, dass die Umgehungsstraße im Punkt B auch „knickfrei" angeschlossen wird. Alle anderen Vorgaben bleiben bestehen. Stellen Sie, soweit möglich, eine ganzrationale Funktion auf, die für die genannten Vorgaben geeignet ist.
Problem/Ansatz: im Anhang ist mein Ansatz, ich habe keine Ahnung was ich falsch mache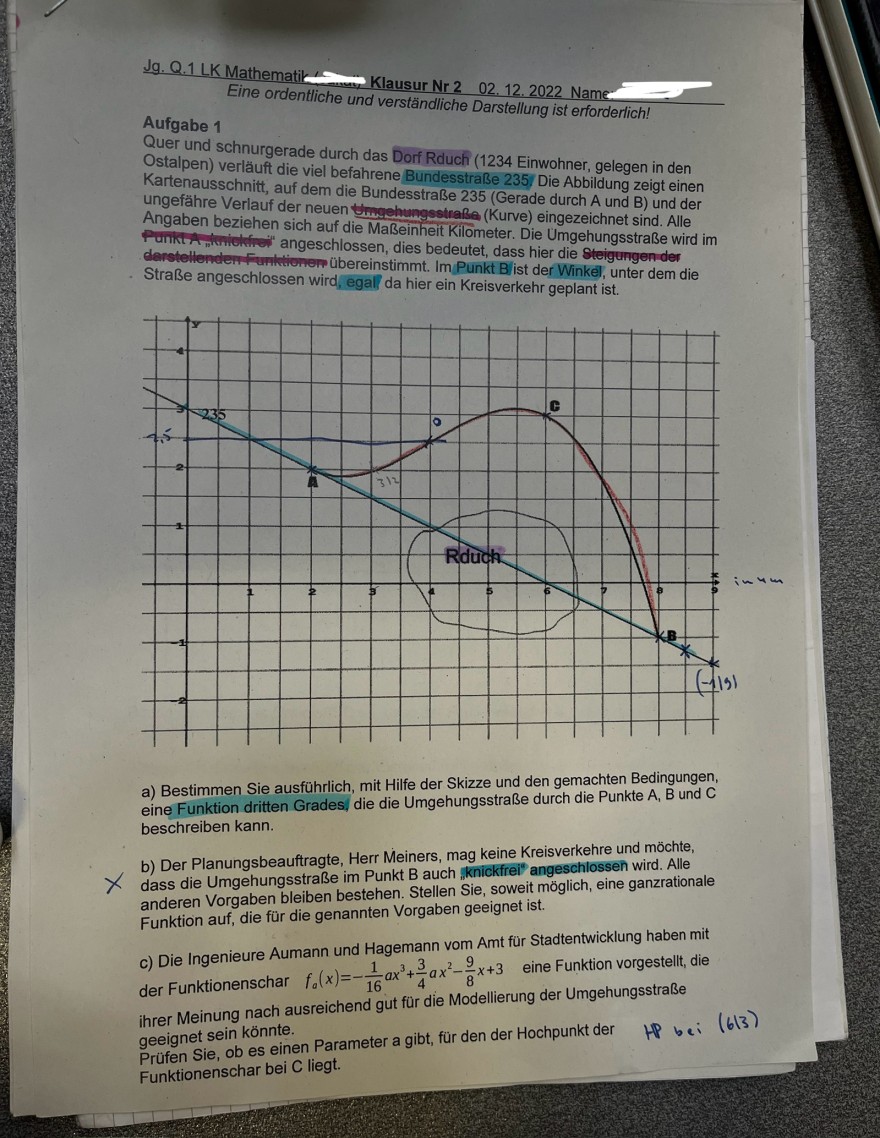
Text erkannt:
Jg. Q. 1 LK Mathematir
Eine ordentliche und verständliche Darstellung ist erforderlich!
Aufgabe 1
Quer und schnurgerade durch das Dorf Rduch (1234 Einwohner, gelegen in den Ostalpen) verlauft die viel befahrene Bundesstraße 235/ Die Abbildung zeigt einen Kartenausschnitt, auf dem die Bundesstraße 235 (Gerade durch A und B) und der ungefähre Verlauf der neuen thmoehungssinaße (Kurve) eingezeichnet sind. Alle Angaben beziehen sich auf die Maßeinheit Kilometer. Die Umgehungsstraße wird im Funkt danstellemenfinhtionem ubereinstimmt. Im Punkt B/ist der Winkel, unter dem die Straße angeschlossen wird, egall" da hier ein Kreisverkehr geplant ist.
a) Bestimmen Sie ausführlich, mit Hilfe der Skizze und den gemachten Bedingungen, eine Funktion dritten Grades, die die Umgehungsstraße durch die Punkte A, B und C beschreiben kann.
b) Der Planungsbeauftragte, Herr Meiners, mag keine Kreisverkehre und möchte, dass die Umgehungsstraße im Punkt B auch "knickfrei" angeschlossen wird. Alle anderen Vorgaben bleiben bestehen. Stellen Sie, soweit möglich, eine ganzrationale Funktion auf, die für die genannten Vorgaben geeignet ist.
c) Die Ingenieure Aumann und Hagemann vom Amt für Stadtentwicklung haben mit der Funktionenschar \( f_{a}(x)=-\frac{1}{16} a x^{3}+\frac{3}{4} a x^{2}-\frac{9}{8} x+3 \) eine Funktion vorgestellt, die ihrer Meinung nach ausreichend gut für die Modellierung der Umgehungsstraße geeignet sein könnte.
Prüfen Sie, ob es einen Parameter a gibt, für den der Hochpunkt der HP bei \( (6 / 3) \) Funktionenschar bei \( \mathrm{C} \) liegt.

Text erkannt:
\( \begin{array}{l}f(8)=-1=a(8)^{4}+b(R)^{3}+c(8)^{2}+d(p)+e=-1 \\ =4096 a+512 b+b 4 c+8 d+c=-1 \\ f(6): 3=a(6)^{4}+b(6)^{3}+(6)^{2}+d(6)+e=3 \\ L C:\{=0,02 ; b=-0,4 ; c=2,21 \quad ; d:=3,5 \quad ; e=3\} \\ =1216 a+2166+36 c+6 d+e=3 \\ f(x)=0,02 x^{4}-0,4,3+2,24+3,5 x+3 \\ f(9)=-1,5=a(9)^{4}+b(0)^{3}+(0)^{2}+d(9)+e=-1,5 \\ =6561 a+72+6+81 c+9 d \text { te }=-1,5 \\\end{array} \)