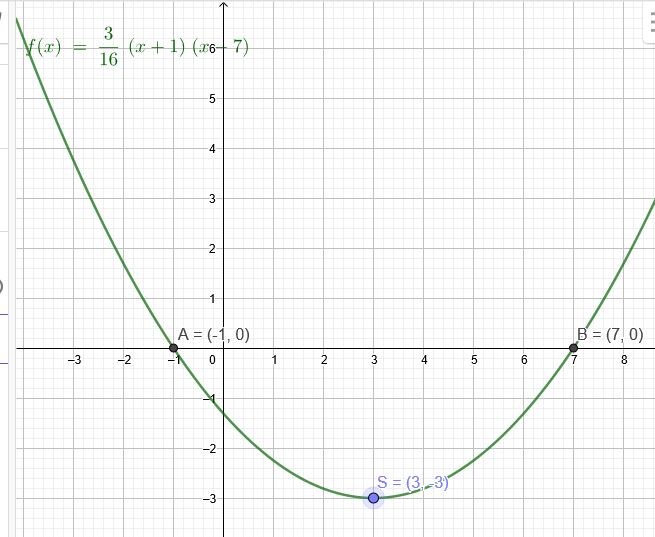
Der Scheitelpunkt der Parabel hat die Stelle \(x=3\) Eine Nullstelle ist bei \(x=-1\) Somit liegt die 2. Nullstelle wegen der Symmetrie bei \(x=7\). Nun kannst du mit der Nullstellenform der Parabel weiter machen.
\(f(x)=a(x+1)(x\red{-7})\)
Der Scheitel liegt bei \(S(3|-3)\)
\(f(3)=a(3+1)(3\red{-7})=a(4)(-4)=-16a\)
\(-16a=-3\) → \(a=\frac{3}{16}\)
\(f(x)=\frac{3}{16}(x+1)(x\red{-7})\)