Hallo,
eine kubische Funktion und ihre Ableitungen kannst du schreiben als
\(f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\)
Du brauchst für die 4 Unbekannten die entsprechende Anzahl an Gleichungen. Nimm die Informationen aus dem Aufgabentext:
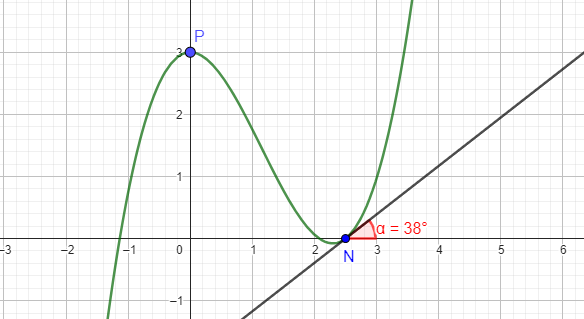
x-Achse wird bei x = 2,5 geschnitten
\(f(2,5)=0\Rightarrow 15,625a+6,25b+2,5 c+d=0\)
Schnittwinkel 38°
\(f'(2,5)=tan(38°)\Rightarrow 18,75a+5b+c=0,78\)
Punkt (0|3)
\(f(0)=3\Rightarrow d=3\)
waagerechte Tangente in diesem Punkt
\(f'(0)=0\Rightarrow c=0\)
In dem Fall ist es geschickter, die letzten beiden Informationen schon in die ersten beiden Gleichungen einzubauen, denn dann bleibt noch das Gleichungssystem
\(15,625a+6,25b=-3\\ 18,75a+5b=0,78\),
das du mit einem Verfahren deiner Wahl lösen kannst.
Gruß, Silvia