Ziehungswahrscheinlichkeit von fünf Kugeln

Question

Aufgabe:

In einem Behälter befinden sich fünf Kugeln. Zwei Kugeln werden nacheinander ohne
Zurücklegen gezogen (dabei wird angenommen, dass jede Ziehung von zwei Kugeln die
gleiche Wahrscheinlichkeit hat). Zwei der fünf Kugeln im Behälter sind blau, die anderen
Kugeln sind rot. Mit p wird die Wahrscheinlichkeit bezeichnet, beim zweiten Zug eine blaue
Kugel zu ziehen.

Geben Sie die Wahrscheinlichkeit p an.

Problem/Ansatz:

Ich hätte mir gedacht, die Lösung ist 3/5*2/4*2, aber laut dem Ergebnis lautet diese p=2/5*1/4+3/5*1/2=2/5

Answer 1

P(rb, bb) = 3/5*2/4 + 2/5*1/4= 6/20+2/20 = 8/20 = 2/5 = 40%

Comments

Das weiß der FS doch bereits. Unnötige Antwort, die nicht auf die Frage des FS eingeht.

Answer 2

Das geht ja nur wenn man rb oder bb zieht.

p(rb) = 3/5 * 2/4  = 3/5 * 1/2

weil erst 3 von den 5en rote da sind und dann nur noch 2 von den 4en blau

p(bb) = 2/5 * 1/4 (erst 2 blaue von 5en dann 1 blau von 4en)

Die Summe ist die gesuchte Wahrscheinlichkeit p.

Answer 3

Zeichne dir zunächst ein Baumdiagramm:

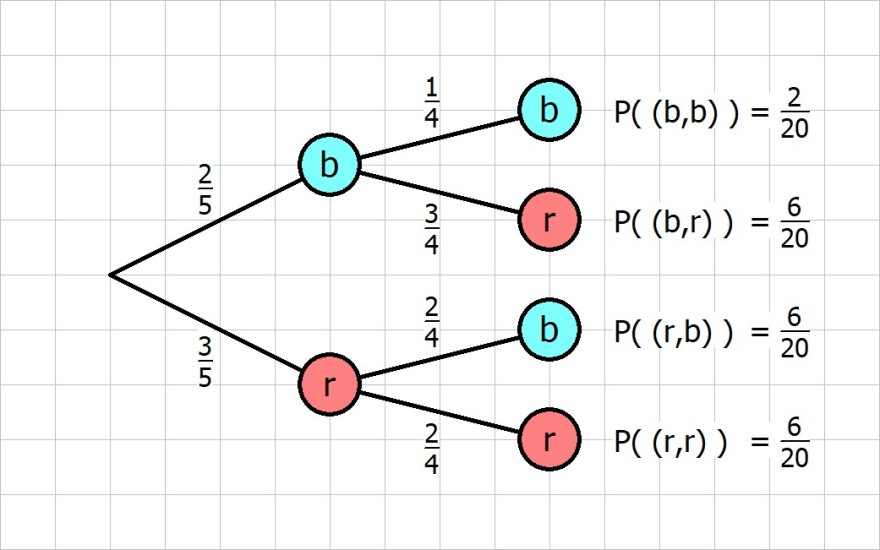
Für die Wahrscheinlichkeit das die zweite Kugel blau ist kannst du alle Pfadwahrscheinlichkeiten addieren bei denen als zweites eine blaue Kugel gezogen wird.

P(2. Kugel blau) = P(bb, rb) = 2/20 + 6/20 = 8/20 = 4/10 = 2/5 = 0.4

Ziehe per Definition die zweite Kugel als erstes aus der Urne, dann ist die Wahrscheinlichkeit für blau auch 2/5.

Das ist hilfreich, wenn man aus einer größeren Urne nicht 2-mal zieht, sondern 100-mal. Die Wahrscheinlichkeit eine blaue Kugel als Erstes zu ziehen ist immer genauso groß wie eine blaue Kugel an jeder anderen der 100 Stellen zu ziehen.