Aufgabe:
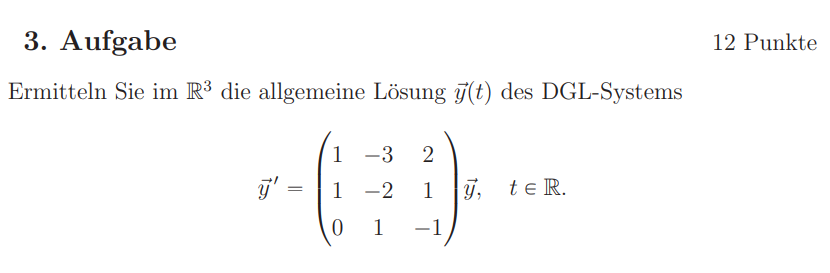
Text erkannt:
3. Aufgabe
12 Punkte
Ermitteln Sie im \( \mathbb{R}^{3} \) die allgemeine Lösung \( \vec{y}(t) \) des DGL-Systems
\( \vec{y}^{\prime}=\left(\begin{array}{ccc} 1 & -3 & 2 \\ 1 & -2 & 1 \\ 0 & 1 & -1 \end{array}\right) \vec{y}, \quad t \in \mathbb{R} \)
Problem/Ansatz:
Hallo, und zwar brauche ich Hilfe bei der bestimmung des charakteristischen Polynoms, warum bekomme ich etwas ganz anderes raus als in der Lösung, kann mir jemand meinen Fehler zeigen oder einen möglichen Rechenweg zeigen?
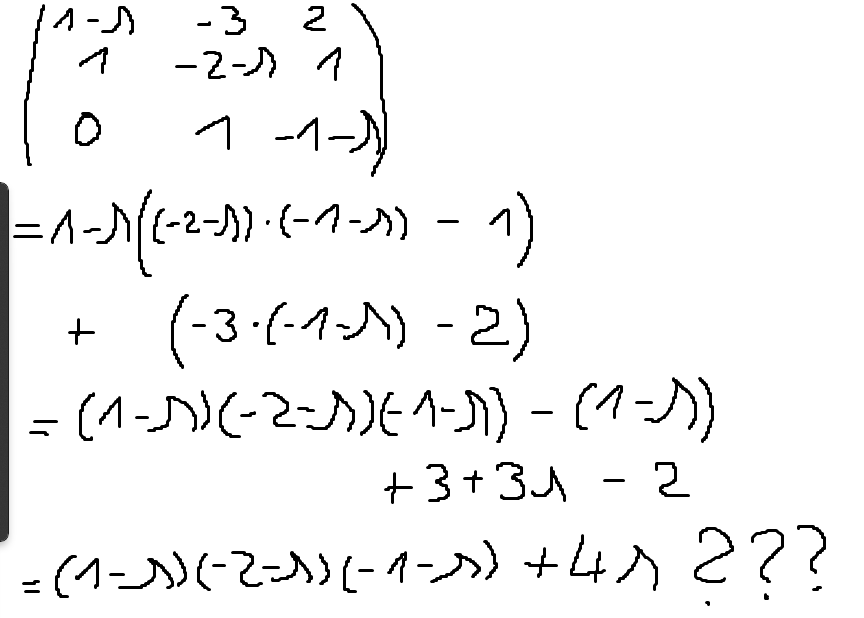
Text erkannt:
\( \begin{array}{l}\left(\begin{array}{ccc}1-\lambda & -3 & 2 \\ 1 & -2-\lambda & 1 \\ 0 & 1 & -1-\lambda\end{array}\right) \\ =1-\lambda((-2-\lambda) \cdot(-1-\lambda)-1) \\ +(-3 \cdot(-1-\lambda)-2) \\ =(1-\lambda)(-2-\lambda)(-1-\lambda)-(1-\lambda) \\ \quad+3+3 \lambda-2 \\ =(1-\lambda)(-2-\lambda)(-1-\lambda)+4 \lambda ? ? ?\end{array} \)
Das sollte eigentlich die Lösung sein:

Text erkannt:
Charakteristisches Polynom
\( \begin{array}{l} \left|\begin{array}{ccc} 1-\lambda & -3 & 2 \\ 1 & -2-\lambda & 1 \\ 0 & 1 & -1-\lambda \end{array}\right|=-\lambda^{3}-2 \lambda^{2}-\lambda \\ \quad=-\lambda\left(\lambda^{2}+2 \lambda+1\right)=-\lambda(\lambda+1)^{2} \end{array} \)
woraus sich der einfache Eigenwert 0 und der doppelte Eigenwert -1 ergeben.