Hilfe bei Polarkoordinaten und kartesische Koordinaten

Question

Aufgabe:

Polarkoordinaten berechnen und in Kartesische Koordinaten umwandeln

Problem/Ansatz:

Hey, hab meinen Ansatz versucht, aber ich komm beim rechnen einfach nicht weiter. meine Zahlen wirken falsch. könnte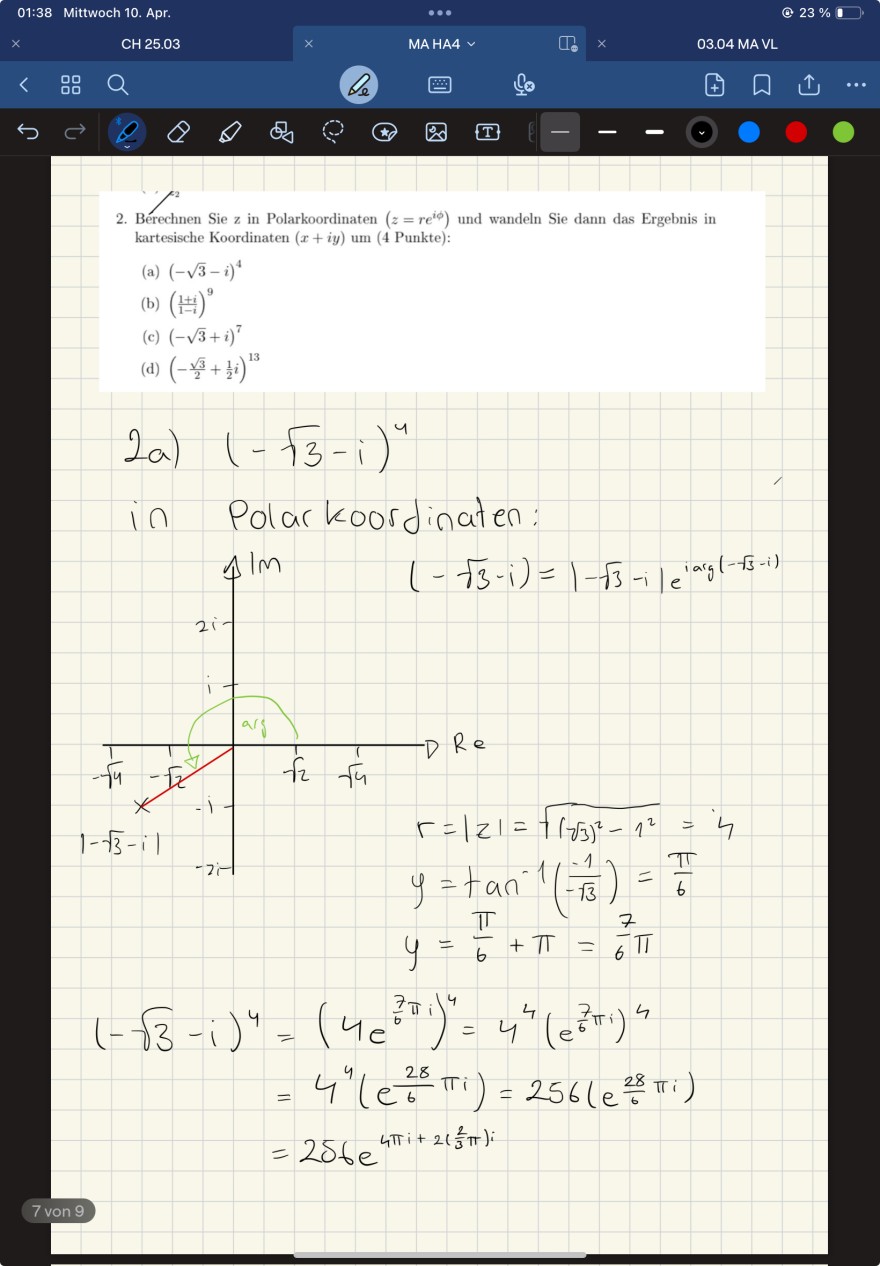

Text erkannt:

2. Bérechnen Sie \( \mathrm{z} \) in Polarkoordinaten \( \left(z=r e^{i \phi}\right) \) und wandeln Sie dann das Ergebnis in kartesische Koordinaten \( (x+i y) \) um (4 Punkte):
(a) \( (-\sqrt{3}-i)^{4} \)
(b) \( \left(\frac{1+i}{1-i}\right)^{9} \)
(c) \( (-\sqrt{3}+i)^{7} \)
(d) \( \left(-\frac{\sqrt{3}}{2}+\frac{1}{2} i\right)^{13} \)
2a) \( (-\sqrt{3}-i)^{4} \)
in Polarkoordinaten:
\( \begin{aligned} |-\sqrt{3}-i|+2 i & =|z|=\sqrt{(\sqrt{3})^{2}-1^{2}}=4 \\ y & =\tan ^{-1}\left(\frac{-1}{-\sqrt{3}}\right)=\frac{\pi}{6} \\ y & =\frac{\pi}{6}+\pi=\frac{7}{6} \pi \\ (-\sqrt{3}-i)^{4} & =\left(4 e^{\frac{7}{6} \pi i}\right)^{4}=4^{4}\left(e^{\frac{7}{6} \pi i}\right)^{4} \\ & =4^{4}\left(e^{\frac{28}{6} \pi i}\right)=256\left(e^{\frac{28}{6} \pi i}\right) \\ & =256 e^{4 \pi i+2\left(\frac{2}{3} \pi\right) i} \end{aligned} \)
7 von 9

jemand drüber schauen?

Answer 1

Berechne nochmal den Betrag. Wie kommst du denn da auf 4? In der Wurzel muss ein + stehen. Der Rest sieht soweit gut aus. Am Ende müsste im Exponenten nicht \(2\cdot\frac{2}{3}\pi\) stehen, sondern \(2\cdot \frac{2}{6}\pi\). Außerdem kannst du hier noch weiter vereinfachen.

Tipp: Kürze Brüche vorher! Es ist \(\frac{28}{6}=\frac{14}{3}\). Jetzt kannst du Vielfache von \(2\pi\) rausrechnen. Dann bleibt im Exponenten \(\frac{2}{3}\pi\mathrm{i}\) übrig.

Comments

Text erkannt:

\( \begin{aligned}(-\sqrt{3}-i)^{4} & =\left(4 e^{\frac{7}{6} \pi i}\right)^{4}=4^{4}\left(e^{\frac{7}{6} \pi i}\right)^{4} \\ & =4^{4}\left(e^{\frac{28}{6} \pi i}\right)=256\left(e^{\frac{28}{6} \pi i}\right) \\ & =256 e^{\frac{14}{3} \pi i}=256 e^{\pi i+2\left(\frac{2}{6} \pi\right) i}\end{aligned} \)

meinen sie es so? und falls ja, wie würde ich damit weiter rechnen. ich verstehe die notizen vom prof nicht ganz

---

Du solltest doch den Betrag prüfen, der ist nicht 4. Und dann Bruchrechnung: schreibe 14/3 als gemischte Zahl. Nach Korrektur geht es weiter mit der Eulerschen Formel (Umwandlung zurück).

---

ist es wurzel aus 2?

---

Nicht raten, rechnen. Hinweis oben beachten.

---

hatte gerechnet nur die klammern falsch gesetzt, hab jetzt 2 raus

---

Das stimmt.     .

---

Text erkannt:

\( \begin{aligned}(-\sqrt{3}-i)^{4} & =\left(2 e^{\frac{7}{6} \pi i}\right)^{4}=2^{4}\left(e^{\frac{7}{6} \pi i}\right)^{4} \\ & =2^{4}\left(e^{\frac{28}{6} \pi i}\right)=16\left(e^{\left.\frac{28}{6} \pi i\right)}\right. \\ & =16 \cdot e^{\frac{14}{3} \pi i}=16 e^{\pi i+2\left(\frac{2}{6} \pi\right)}\end{aligned} \)

mein problem ist, dass ich nicht weiß wie ich von hier aus weiter rechnen kann. Upload failed: [object Object]

---

Lies die Tipps, oben steht wie's weitergeht (Bruchrechnung, Eulersche Formel usw.).

---

Rechne die Vielfachen von \(2\pi\) heraus. Es steht aber auch alles in der Antwort. Dein letzter Schritt stimmt nicht und \(2\cdot \frac{2}{6}\) kann man auch noch vereinfachen.

Weiterer Tipp für die Zukunft: Vereinfache deine Rechnungen immer so weit wie möglich. Wenn es geht, so früh wie möglich.

Answer 2

Falls keine vorherige Umwandlung in Polarkoordinaten verlangt ist:

\( (\frac{1+i}{1-i})^{9} \)

Einschub:

\( \frac{1+i}{1-i}= \frac{(1+i)(1+i)}{(1-i)(1+i)}=\frac{1+2i+i^2}{1-i^2}=\frac{1+2i-1}{1+1}=i \)

\( (\frac{1+i}{1-i})^{9}=i^9=i \)

Comments

vielen Dank Ihnen!

---

Ist es aber! Dafür gäbe es von mir keine volle Punktzahl!

---

warum denn? fehlt ein rechenschritt? es sieht aber komplett aus

---

Weil die Aufgabe auch verlangt, das Ergebnis in Polarkoordinaten anzugeben.

---

hab grad versucht r auszurechnen aber mit ((1+1)/(1-1))² geht es nicht, da wir ja nicht durch 0 teilen können

---

Du musst ja zunächst auf die Darstellung \(a+b\mathrm{i}\) kommen. Du kannst hier nicht einfach den Betrag vom Zähler und Nenner getrennt betrachten.

---

hmm okay ich probiers mal gleich, vielen Dank!

---

Ist es aber! Dafür gäbe es von mir keine volle Punktzahl!

Darum habe ich auch den Grüneintrag dazugeschrieben!