Aufgabe:
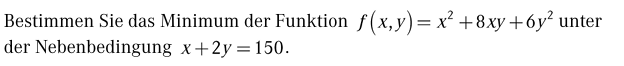
Text erkannt:
Bestimmen Sie das Minimum der Funktion \( f(x, y)=x^{2}+8 x y+6 y^{2} \) unter der Nebenbedingung \( x+2 y=150 \).
Problem/Ansatz:
Gelöst werden soll die Aufgabe mit dem Lagrange Ansatz. Ich bin neu in dem Thema und habe mal meine aktuelle Rechnung aufgeschrieben. Konkret habe ich 4 Fragen..
1 Frage) Ich habe 8+12y=-2λ wie löse ich hier weiter auf?
2 Frage) in der nächsten Zeile habe ich x+12 =-2λ-> Hier meine Frage, wie löse ich das auf, wenn ich auf der linken Seite zwei variablen stehe habe?
3 Frage) Man könnte es laut Buch auch lösen, indem man den λ Parameter entfernt, indem man die 1. Zeile * 2 nimmt und diese Subtrahiert wird von der zweiten Zeile. Anschließend setzt man die erhaltene Gleichung in die 3 Gleichung ein. Hier meine Frage, warum überhaupt in die dritten Gleichung und nicht in die zweite ?
4) Wenn ich schaffe im Gleichungssystem den λ Parameter verschwinden zu lassen, kann ich es dann immer in ein beliebiges gleichungssystem einsetzen, ausrechnen und komme dann auf die Lösung?
Text erkannt:
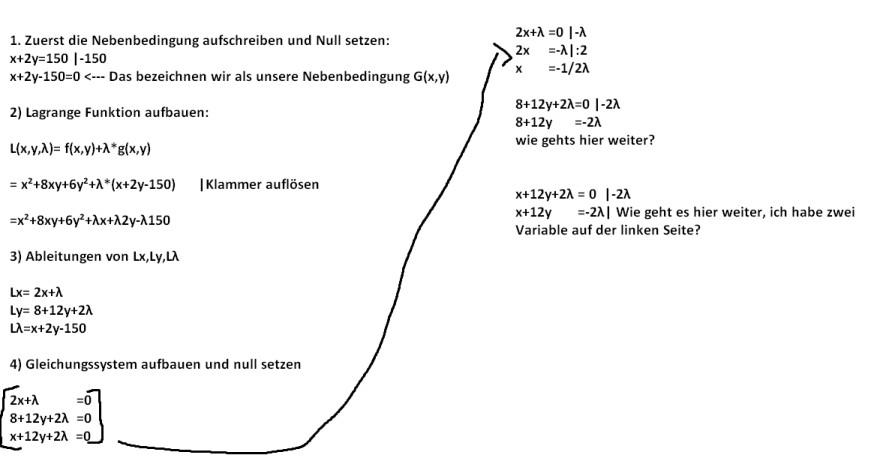
1. Zuerst die Nebenbedingung aufschreiben und Null setzen: \( x+2 y=150 \quad \mid-150 \)
\( x+2 y-150=0 \) <--- Das bezeichnen wir als unsere Nebenbedingung \( G(x, y) \)
2) Lagrange Funktion aufbauen:
\( \begin{array}{l} L(x, y, \lambda)=f(x, y)+\lambda^{*} g(x, y) \\ =x^{2}+8 x y+6 y^{2}+\lambda^{*}(x+2 y-150) \quad \mid \text { Klammer auflösen } \\ =x^{2}+8 x y+6 y^{2}+\lambda x+\lambda 2 y-\lambda 150 \end{array} \)
3) Ableitungen von \( L x, L y, L \lambda \)
\( \begin{array}{l} L x=2 x+\lambda \\ L y=8+12 y+2 \lambda \\ L \lambda=x+2 y-150 \end{array} \)
4) Gleichungssystem aufbauen und null setzen
\( \left[\begin{array}{ll} 2 x+\lambda & =0 \\ 8+12 y+2 \lambda & =0 \\ x+12 y+2 \lambda & =0 \end{array}\right] \)
\( 2 x+\lambda=0 \mid-\lambda \)
\( 2 x=-\lambda \mid: 2 \)
\( \begin{array}{l} x=-1 / 2 \lambda \\ 8+12 y+2 \lambda=0 \quad \mid-2 \lambda \\ 8+12 y \quad=-2 \lambda \end{array} \)
wie gehts hier weiter?
\( x+12 y+2 \lambda=0 \quad \mid-2 \lambda \)
\( x+12 y=-2 \lambda \mid \) Wie geht es hier weiter, ich habe zwei Variable auf der linken Seite?